研究開発部の浅野です。普段は画像やヘルスケアデータを扱うことが多いのですが、最近シフトスケジューリング問題に興味をもって学び始めたので、その内容を少しご紹介したいと思います。シフトスケジューリング問題とは、人員の配置基準や働く人の希望、能力、相性、業務負荷などを加味しながらある一定期間(1ヶ月など)の勤務シフト表を作成する問題です。看護師のナーススケジューリングが有名ですが、保育士のシフト作成も多くの園長先生が頭を悩ませていることの一つです。今回はこの問題を最適化問題としてモデル化・定式化して実際に解いてみたいと思います。
最適化問題は、制約条件を満たす解の中で、目的関数を最小(最大)にする解を求めるもので、次のように定義されます。
\begin{align} minimize \quad &f(x): &目的関数\\ subject \; to \\ &g(x)>= 0: &不等式制約条件\\ &h(x) = 0: &等式制約条件\\ &a <= x <= b: &変数\\ \end{align}
我が家のシフトスケジューリング問題
共働きで3人の子どもを育てており、朝の支度と夜のお迎えから寝かしつけまでを夫婦どちらが担当するのか、仕事などの都合を考慮して決めています。週の終わりにお互いの来週の予定を共有し、それをもとに1週間分のシフトを作成します。それぞれの都合を尊重しつつ公平性を保った配分を手作業で決めるのは結構面倒です。
それではこの問題を徐々にモデル化および定式化していきましょう。メンバーが曜日
にアクション
を担当するときに
、そうでないときに
となる変数
を使います。夫婦がどちらも都合が悪い場合に奥様の母上がヘルプに入ってくれてとても助かっているのですが、それに甘えすぎると大切な子どもとの時間を仕事などに割り振ってしまう傾向が強まります。そこで目的関数として母上のヘルプ回数を設定し、それを最小化するという問題設定にします。
これは我が家ではこうするのがよい、ということであり、各家庭の状況によって問題設定は変わります。このように、どんな目的関数を設定してどのような制約条件を設けるかというモデリングはかなりドメインの知識を必要とする作業です。
それではここまでの部分をコードに落としてみましょう。PythonのPuLPという最適化問題のモデリングを簡単にコーディングできるライブラリを用います。PuLPには汎用ソルバーもバンドルされているため、そのまま解を求めることも可能です。
import pulp Member = ["夫", "妻", "母"] Day = ["Mon", "Tue", "Wed", "Thu", "Fri"] Action = ["朝", "お迎え"] #問題の宣言 ShiftScheduling = pulp.LpProblem("ShiftScheduling", pulp.LpMinimize) #変数宣言 x = {} for m in Member: for d in Day: for a in Action: x[m, d, a] = pulp.LpVariable("x({:},{:},{:})".format(m,d,a), 0, 1, pulp.LpInteger) #目的関数:母からのヘルプを最小限に抑える ShiftScheduling += pulp.lpSum(x['母', d, a] for d in Day for a in Action), "Target"
制約条件
制約条件として、まず下記を考えます。
これは毎日朝とお迎えには誰か1人が必ずアサインされる、という意味です。そうしないと子ども達が路頭に迷ってしまいます。次に、この日は朝早く出社したい、あるいは遅くなるからお迎えに行けない、といった条件を加えます。
これらをコードにすると下記のようになります。夫は火曜朝と木曜夜、妻は水曜夜、(宿泊出張で)木曜夜と金曜の朝が都合が悪い(実際よくあるパターン)、としています。
# それぞれの日の朝やお迎えに必ず誰か1人が割り当てられる for d in Day: for a in Action: ShiftScheduling += pulp.lpSum(x[m, d, a] for m in Member) == 1, "Constraint_{:}_{:}".format(d,a) # 対応不可能日 NG = [['夫','Tue','朝'],['妻','Wed','お迎え'],['夫','Thu','お迎え'],['妻','Thu','お迎え'],['妻','Fri','朝']] for m, d, a in NG: ShiftScheduling += x[m, d, a] == 0, "Constraint_NG_{:}_{:}_{:}".format(m,d,a)
解いてみる
では一旦この状態で最適化問題を解いてみましょう。関数を呼ぶだけです。その結果作成されたシフトも示します。
results = ShiftScheduling.solve() print("optimality = {:}, target value = {:}".format(pulp.LpStatus[results], pulp.value(ShiftScheduling.objective)))

print文の出力は、最適解が見つかったことと、母上の出動が1回あることを示しています。確かに木曜のお迎えは夫婦どちらも対応できないのでやむを得ません。他の都合が悪い日についてもちゃんと考慮されたシフトになっています。ただしこれをこのまま奥様に見せたら不公平だとお怒りになりますね。
制約条件の追加
そこで1週間の出動回数の差が大きくならないように制約条件を追加します。数式は割愛してコードと結果を示します。
# 週全体で出動回数の差を抑える n_act_wife = pulp.lpSum(x['妻', d, a] for d in Day for a in Action) n_act_husband = pulp.lpSum(x['夫',d, a] for d in Day for a in Action) ShiftScheduling += n_act_wife - n_act_husband <= 1, "Constraint_fairness_wife" ShiftScheduling += n_act_husband - n_act_wife <= 1, "Constraint_fairness_husband"
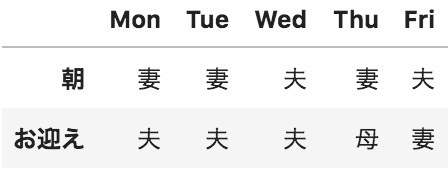
これで奥様の怒りも収まりますね。しかしよく見ると水曜日は朝もお迎えも自分が担当になっていて、できなくはないのですがちと辛い。そこでもう一つ制約条件を加えて朝とお迎えが重ならないようにします。ここも数式は割愛。
# 1日で朝かお迎えどちらかだけ for m in Member: for d in Day: ShiftScheduling += pulp.lpSum(x[m, d, a] for a in Action) <= 1, "Constraint_Either_{:}_{:}".format(m,d)

いいシフトができました。今後は都合の悪い日をインプットするだけで自動的に公平な分担表を作成できて楽になります。
まとめ
シフトスケジューリング問題に対して、最適化問題としてのモデル化、定式化、コードへの実装を一通り行うことができました。今回扱ったのは登場メンバーが3人で1週間分の朝とお迎えシフトを決めるという比較的小さな問題で、変数の数が30しかないため解は一瞬で得られます。実際の保育士のシフト作成は、数十人の保育士さんの1ヶ月分の勤務(早番、中番、遅番など)を、園児の人数あたりの保育士配置基準、ベテランと若手のミックス、研修や休暇などの予定、シフトに入れる時間帯の制約、体調などを考慮に入れて作成します。変数の数や制約条件が桁違いに多くなるため複雑な作業になりますが、ドメイン知識を使ってモデル化し、目的関数や制約条件をうまく定式化し、ソルバーを使って解くという流れは同じです。こうした技術を使って保育園での作業負担をどんどん減らしていきたいですね。