Q-Learning.
By Matthew Millar R&D Scientist at ユニファ
Q -learning is a model-free approach to reinforcement learning. This means that Q-learning does not rely on a model to make decisions based on an input, but instead uses a policy that shows the agent what actions to perform given a certain circumstance. Q-learning should find the best policy which gives an optimal solution to any finite Markov decision process. The FMDP can be described as: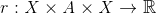
Where X is the state space, A is the action space, and r is the reward function. The optimal solution is obtained by maximizing the total reward for any action and any change in state, starting with the current state. The best or optimal solution can be found for any finite problem given an unlimited exploration time combined with an exploration adaption to a policy. This optimal Q-function can be calculated as such:
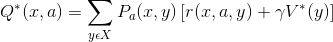
The full equation and explanation can be found in Melo’s Convergence of Q-Learning: A Simple Proof [1]:
Influences on how the agent will learn using Q-learning comes down to three real factors. Learning rate controls how much, or the rate in which new information replaces older information. If the learning rate is set to 0, then the agent will never learn anything new and will rely on previous knowledge to choose its actions. If the rate is set to 1, then the agent will only look at the most recent data and completely discard previous data.
The Discount factor is another variable that controls learning. The discount factor determines the weight of future rewards and how important or not these rewards will be. If it is set to 0, then the model will only consider instant rewards or the current reward and not look towards potential rewards of future actions. If the discount factor is set to 1, then the agent will work towards achieving the long-term highest reward.
The third and final variable used for learning the control is the initial conditions or Q0. Q-learning is an iterative program, it must have a starting condition before any changes take place to any state or environment. To help an agent explore options better, high initial values should be used regardless of which action is used. The update rules can control the values compared to other alternatives which can increase its total probability of being chosen. This will allow for each option to be fully explored and to aid in finding an optimal solution to each problem.
Q-Tables:
Q-Learning runs off a table or matrix of state and actions. This Q-table starts out all values as 0 and after each episode, these values are updated accordingly. The matrix should take the size of both the state as well as the action size with a very basic form of this is a simple array [state, action]. The simplest method for creating a Q-table in python is this:
import numpy as np # Initial Q-table Q_table = np.zeros((state_size, action_size))
This Q-table will store every action and state that the agent will be in. Exploitation is done when an action that has been performed before and in a certain state is chosen which results in a reward (most likely the max possible future reward). Exploration is choosing a random action at any point in time and in any state. A basic method for this could be defined as below:
import random epli = 0.4 def choose_action (epli):: ran_float = random.random() # Generates a random float between [0,1] if ran_float < epli: #preform a random action else: get_action_from_qtable(current_state, q_table)
After choosing an action to perform and receiving a reward, the Q-table must be updated. The updating must be done after each action is performed. The updating phase will end at the conclusion of each episode. The basic flow of the update function will be:
Step 1: Get the current state of the agent.
Step 2: The agent takes action. (Picks random action or Pick action from Q-table)
Step 3: Update q-value.
An update rule for Q-values can be described as:
Q[state, action] = Q[state, action] + learning_rate * (reward + gamma * np.max(Q[new_state, :])) – Q[state, action]
This is a basic approach to adjust and update q-values in a Q-table.
Now for a simple example:
First lest look at the agent in the game:
class Agent: def __init__(self, learning_rate = 0.1, discount = 0.95, exploration_rate = 1.0, iterations = 1000): # Q talbe for holding rewards self.q_table = [[0,0,0,0,0], [0,0,0,0,0]] self.learning_rate = learning_rate self.discount = discount # Future rewards value to current rewards self.exploration_rate = exploration_rate # Exploration rate # This controls sift from exploration to exploation self.exploration_delta = 1.0 / iterations # Chose between explotation or exploration def get_next_action(self, state): if random.random() > self.exploration_rate: return self.greedy_action(state) else: return self.random_action() def greedy_action(self, state): # Check to see if forward is best reward if self.q_table[FORWARD][state] > self.q_table[BACKWARD][state]: return FORWARD elif self.q_table[BACKWARD][state] > self.q_table[FORWARD][state]: return BACKWARD # Rewards are equal, take random action return FORWARD if random.random() < 0.5 else BACKWARD def random_action(self): return FORWARD if random.random() < 0.5 else BACKWARD def update(self, old_state, new_state, action, reward): old_value = self.q_table[action][old_state] # best next action future_action = self.greedy_action(new_state) # reward for the best next action future_reward = self.q_table[future_action][new_state] # Main Q-table updating algorithm new_value = old_value + self.learning_rate * (reward + self.discount * future_reward - old_value) self.q_table[action][old_state] = new_value # Finally shift our exploration_rate toward zero (less gambling) if self.exploration_rate > 0: self.exploration_rate -= self.exploration_delta
Then lets built the environment that he can walk through.
# Build the Environment class EnvironmentSimulator: def __init__(self, length=5, small=2, large=10): self.length = length # Length of the environment self.small = small # reward for going back to the start self.large = large # reward for reaching the end self.state = 0 # environment entry point def take_action(self, action): if action == BACKWARD: reward = self.small self.state = 0 elif action == FORWARD: if self.state < self.length - 1: self.state += 1 reward = 0 else: reward = self.large return self.state, reward # Reset the environment def reset(self): self.state = 0 return self.state
This is a very simple array of 5 spaces. So basically, the agent can walk back a forth and get a reward for either reaching one end or the other.
Next, we will set up the environment and the main loop for running the simulation.
# Set up environment environment = EnvironmentSimulator() environment.reset() # Scores total_reward = 0 last_total = 0 for step in range(iterations): # Store the current state in old state old_state = environment.state action = agent.get_next_action(old_state) new_state, reward = environment.take_action(action) agent.update(old_state, new_state, action, reward) total_reward += reward if step % 250 ==0: performance = (total_reward - last_total) / 250.0 print("Step:{} Performance:{} Total-reward:{}".format(step, performance, total_reward))
RI Hello World Revisited
Let's take a look back at the Cart Pole example from the previous blog,
tech.unifa-e.com
We did that with a Keras model, now we will do it with a q-table approach.
First we need to set up the Q-learning class
class QLearn: def __init__(self, actions, epsilon, alpha, gamma): self.q = {} self.epsilon = epsilon self.alpha = alpha self.gamma = gamma self.actions = actions
Next, we need a few methods for choosing actions and updating the tables:
# Q learning function def learnQ(self, state, action, reward, value): old_value = self.q.get((state, action), None) # If there are no values in the table add the reward if old_value is None: self.q[(state, action)] = reward else: self.q[(state, action)] = old_value + self.alpha * (value - old_value) def chooseAction(self, state): q = [self.getQ(state, a) for a in self.actions] maxQ = max(q) if random.random() < self.epsilon: minQ = min(q); mag = max(abs(minQ), abs(maxQ)) q = [q[i] + random.random() * mag - .5 * mag for i in range(len(self.actions))] maxQ = max(q) count = q.count(maxQ) if count > 1: best = [i for i in range(len(self.actions)) if q[i] == maxQ] i = random.choice(best) else: i = q.index(maxQ) action = self.actions[i] return action, q def learn(self, s1, action, reward, s2): maxqnew = max([self.getQ(s2, a) for a in self.actions]) self.learnQ(s1, action, reward, reward + self.gamma*maxqnew)
And now let's define the main method:
if __name__ == '__main__': # Load the cart pole game from gym ai env = gym.make('CartPole-v0') # Vriables needed max_number_of_steps = 200 last_time_steps = numpy.ndarray(0) n_bins = 8 n_bins_angle = 10 max_number_episodes = 200 episode_number = 0 render = False number_of_features = env.observation_space.shape[0] last_time_steps = numpy.ndarray(0) # Simplfy the number of states as it is too large cart_position = pandas.cut([-2.4, 2.4], bins=n_bins, retbins=True)[1][1:-1] pole_angle = pandas.cut([-2, 2], bins=n_bins_angle, retbins=True)[1][1:-1] cart_velocity = pandas.cut([-1, 1], bins=n_bins, retbins=True)[1][1:-1] angle_rate = pandas.cut([-3.5, 3.5], bins=n_bins_angle, retbins=True)[1][1:-1] qlearn = QLearn(actions=range(env.action_space.n), alpha=0.5, gamma=0.90, epsilon=0.1) while episode_number < max_number_episodes: observation = env.reset() cart_position, pole_angle, cart_velocity, angle_rate_of_change = observation state = build_state([to_bin(cart_position, cart_position), to_bin(pole_angle, pole_angle), to_bin(cart_velocity, cart_velocity), to_bin(angle_rate_of_change, angle_rate)]) for t in range(0, max_number_of_steps): if render: env.render() action = qlearn.chooseAction(state) observation, reward, done, info = env.step(action) cart_position, pole_angle, cart_velocity, angle_rate_of_change = observation nextState = build_state([to_bin(cart_position, cart_position), to_bin(pole_angle, pole_angle), to_bin(cart_velocity, cart_velocity), to_bin(angle_rate_of_change, angle_rate)]) if not(done): qlearn.learn(state, action, reward, nextState) state = nextState else: # Penalize it for failing reward = -200 qlearn.learn(state, action, reward, nextState) last_time_steps = numpy.append(last_time_steps, [int(t + 1)]) break
And that is really the only difference between the Keras and q-learning ways of solving the Cart Pole problem.
Instead of the model deciding what to do, the values in the q-table are making the decision.
Conclusion
This shows how to simply set up an environment and use a q-table to learn RI. This was a simple example the next logical step would be to have a negative reward which would encourage the AI to stop moving backward and to only move forward. This could help shape how the AI will learn and help move it towards the desired actions. This program is really a bare-bones approach with no bells and whistles. It shows you what is the minimum to have for an agent, environment, and simulation for training up a RI agent.
We also revisited the cart pole example to see how Q-Learning can be done compared to using a Keras model. The Keras model needs less code and can solve the issue a little better than the Q-learning approach. This may be because I had to simplify the states that the pole can take which may lead to the poorer results.
Q-learning has its limits as the table can become very complex as the states and actions that are a possible increase in the total number. This can greatly increase the complexity of the Q-table which can become very difficult to manage. By simplifying the dimensions of the state/action sets can help make it more manageable, but you sacrifice granularity which can lead to mistakes in the results.
Resources:
[1]: Melo, F. Convergence of Q-learning: a simple proof. Retrieved 2019 from