ユニファ開発者ブログ

ユニファ株式会社プロダクトデベロップメント本部メンバーによるブログです。

基本的なサンプリングアルゴリズムである棄却サンプリングを試してみた

はじめに

こんにちわ、研究開発部の島田です。今回は統計的学習で基本的なサンプリングアルゴリズムを一つ紹介します。

統計的学習におけるサンプリング手法はいくつかありますが、大別するとマルコフ連鎖モンテカルロ法（MCMC）を使わないサンプリング手法とMCMCを使ったサンプリング手法に分けられます。

MCMCを使わないサンプリング手法の最も基本的なアルゴリズムとして、棄却サンプリングがあげられます。このアルゴリズムは難しい数式を必要としないので、直感的にもわかりやすいです。

今回はこの棄却サンプリングについて簡単な説明と実装を行います。

棄却サンプリング

ベイズ統計でやりたいことは、ある複雑な事後分布からモンテカルロ法を使ってサンプリングをしたいということになります。

そして棄却サンプリングでは、直接事後分布からサンプリングすることは難しいのでもっと単純な分布（これを提案分布と言います）を利用しようという手法です。

ここで、予測分布をp(z)、提案分布q(z)とすると、

p(z) \leq Mq(z)

上の条件を満たすMおよびq(z)を求める必要があります。この条件は予測分布が提案分布をM倍した分布に覆われていることを意味しています。

棄却サンプリングの手順は非常にシンプルで、下記のようになります。

  1. 提案分布q(z)に従う乱数yを発生
  2. [0, Mq(y)]に従う乱数sを発生
  3. s \leq p(y)の場合は受理。そうでない場合は棄却。
  4. 1から3をN回繰り返す。

ベータ分布

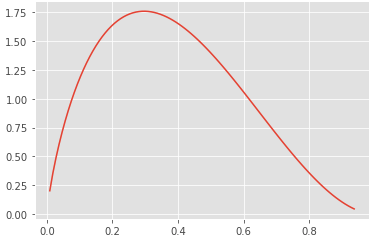
今回は予測分布をベータ分布として棄却サンプリングを試してみます。 ベータ分布とは、確率密度関数が下記の式で表される確率分布のことです。

f(x|α,β) = \dfrac{x^ {α-1}(1-x)^ {β-1}}{B(α, β)}

ただし、α, βは正の実数のパラメータです。 また、ベータ分布は区間[0, 1]上の連続型の確率分布であることが特徴です。 では、ベータ分布の形を確認するためにScipyというPythonライブラリを使って確認してみます。

まずは必要なライブラリのインポートです。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from scipy import optimize as opt
from scipy.stats import beta, uniform

次にベータ分布を描画してみます。必要なコードはたったこれだけです。

np.random.seed()

a, b = 1.8, 2.9
x = np.linspace(beta.ppf(0.001, a, b), beta.ppf(0.999, a, b), 100)
plt.plot(x, beta.pdf(x, a, b))

f:id:unifa_tech:20190816113156p:plain

棄却サンプリングの実行

では、いよいよ棄却サンプリングを試してみます。

提案分布はどんな分布であっても構わないのですが、今回はサンプリングが簡単で理解もしやすい一様分布とします。

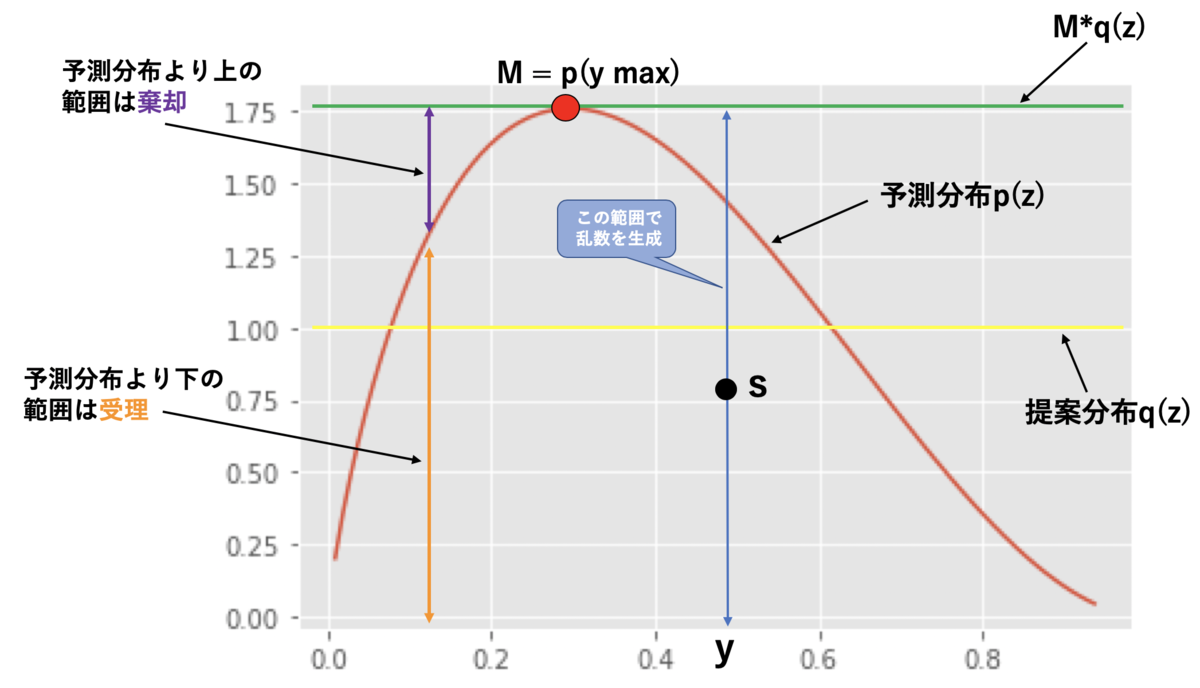
まずは定数Mを求める必要があるのですが、下の図からわかるようにMはベータ分布の最大値p(y max)と求めることが出来ます。

そして、横軸方向について一様分布q(z)からランダムな値yを決めます。具体的には0から1の間で一つ値を決定することになります。

次に縦軸方向については[0, Mq(y)]の一様分布に従ってランダムな値sを決めます。

この処理によって横軸と縦軸のスケールの異なる一様分布から生成された二つの乱数によって座標が一点決まることになります。

そしてこの乱数によって求まった値sが予測分布よりも下の範囲であれば採用します。とてもシンプルですね！

当然ながらサンプリング数が多ければ多いほど、予測分布に近しい結果になります。

f:id:unifa_tech:20190816153734p:plain:w600

では、実装して結果を見ていきます。

まずはMを求めますが、今回はScipyのOptimize関数を使います。ScipyのOptimize関数は目的関数を最適化（最小値もしくは最大値を求める）する便利な関数です。

f = beta(a=a, b=b).pdf
res = opt.fmin(lambda x: -f(x), 0.1)
M = f(res)
print("M : ", M)

f:id:unifa_tech:20190816113912p:plain:w300

f(x)にマイナスをつけているのは、ベータ分布の最大値を求めるために最小値問題に帰着させるためです。

結果を見てみると上手くベータ分布の最大値を求められていることがわかります。

次に乱数を生成して提案分布が予測分布に近しい結果になっていくことを確認します。

まずは乱数を1000個生成した場合を見てみます。

N_MC = 1000

y = uniform.rvs(size=N_MC)
mq = M * uniform.rvs(size=N_MC)
accept = y[mq <= f(y)]

plt.hist(accept, normed=True, bins=35, rwidth=0.8, label="rejection sampling")
x = np.linspace(beta.ppf(0.001, a, b), beta.ppf(0.999, a, b), 100)
plt.plot(x, beta.pdf(x, a, b), label="target distribution")
plt.legend()

f:id:unifa_tech:20190816114630p:plain:w400

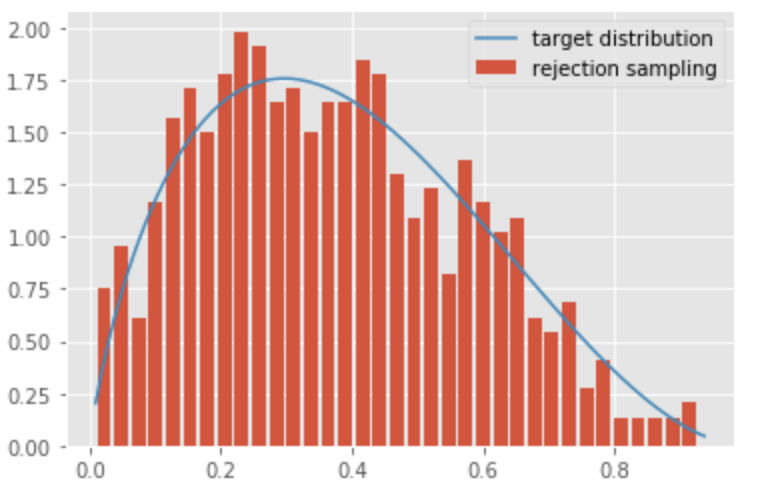
1000個の乱数だと、まだ少し予測分布（ベータ分布）に対して少しバラツキがありますね。

では、乱数を50000個に増やしてみましょう。

f:id:unifa_tech:20190816114751p:plain:w400

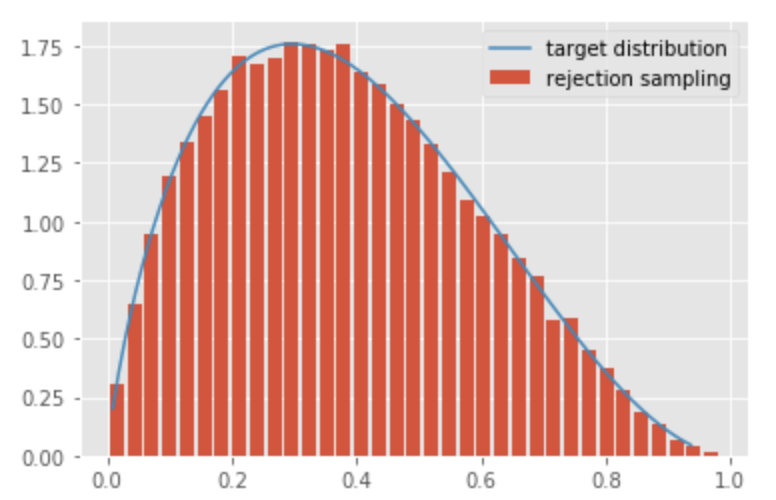
すると、乱数が1000個に比べてベータ分布に対してほぼ同じような曲線を描いていることがわかります。

最後に

今回は基本的なサンプリングアルゴリズムである棄却サンプリングを試してみました。異なる分布から求めたい分布のサンプルを非常にシンプルな考えで得ることが出来て面白いですね。サンプリングアルゴリズムは他にもたくさんあるので、是非試してみたいと思います。