こんにちは、研究開発部の浅野です。あるプロダクトで、得られる時系列データが正常か異常かを判定しているところがあります。現在はシンプルなルールベースの手法で判断をしており、その精度は約80%と改善が必要です。今回はこれを向上していきたいと思います。幸い正常例も異常例もデータが比較的多くあるため、機械学習の手法を用いることにします。
使用データ
正常例と異常例を約1,000例ずつ手作業で集めました(データ収集, クレンジング, ラベリングは辛いときもありますが大事なタスクの一つです)。そのうち80%を学習用データ、20%をテスト用データとしました。下記の例を見るとすぐに規則性を見出すのは難しそうですが、異常例の方が全体的に値が高めに出る傾向にはありそうですね。

手法
決定木ベースのアンサンブル学習手法で、汎化性能が高く動作も高速なランダムフォレストを使用します(コードはscikit-learnを使えば自明なので特に示していません)。とかくブラックボックス(判断根拠がわかりにくい)と言われがちな機械学習ですが、決定木ベースの手法を用いるとそのあたりはかなり軽減することができます。
データをざっと眺めてみると、最大の値とばらつき具合が判断に大きく寄与しているように感じたので、まずは最大値と標準偏差の値を特徴量として分類器を作成してみます。2つしか特徴量がないので木の深さの最大値は2、決定木の数は3として学習を行いました。
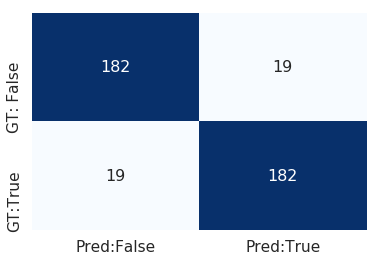
特徴量を増やす
もっと精度を高めるため、関連しそうな特徴量を追加していきます。具体的には、最小値、平均値、中央値、歪度(skewness)、尖度(kurtosis)といったデータの分布に関わる統計指標です。特徴量が増えるので決定木の深さを最大3,数を10として学習したところ次のような結果になりました。
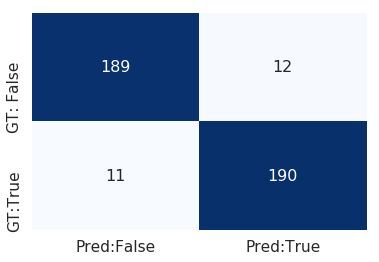
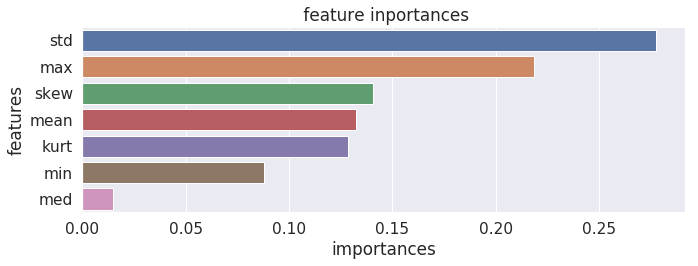
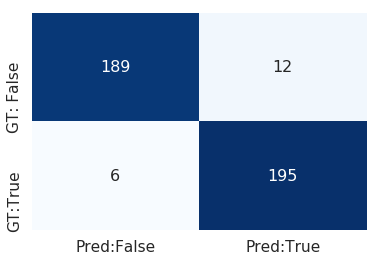 さらに、「最大値ー平均値」や「平均値ー最小値」などのようにより直接的に分布の歪みを捉えることができるような特徴量を追加したり、汎化性能を高めるために不要な特徴量を削除することで混同行列が左のようになり、最終的に異常なデータの検出においてprecision: 94%, recall:97%, f1-score: 96%まで精度を改善することができました。このあたりの特徴量エンジニアリングは機械学習に携わる者として腕の見せ所の一つです。
さらに、「最大値ー平均値」や「平均値ー最小値」などのようにより直接的に分布の歪みを捉えることができるような特徴量を追加したり、汎化性能を高めるために不要な特徴量を削除することで混同行列が左のようになり、最終的に異常なデータの検出においてprecision: 94%, recall:97%, f1-score: 96%まで精度を改善することができました。このあたりの特徴量エンジニアリングは機械学習に携わる者として腕の見せ所の一つです。
決定木の可視化
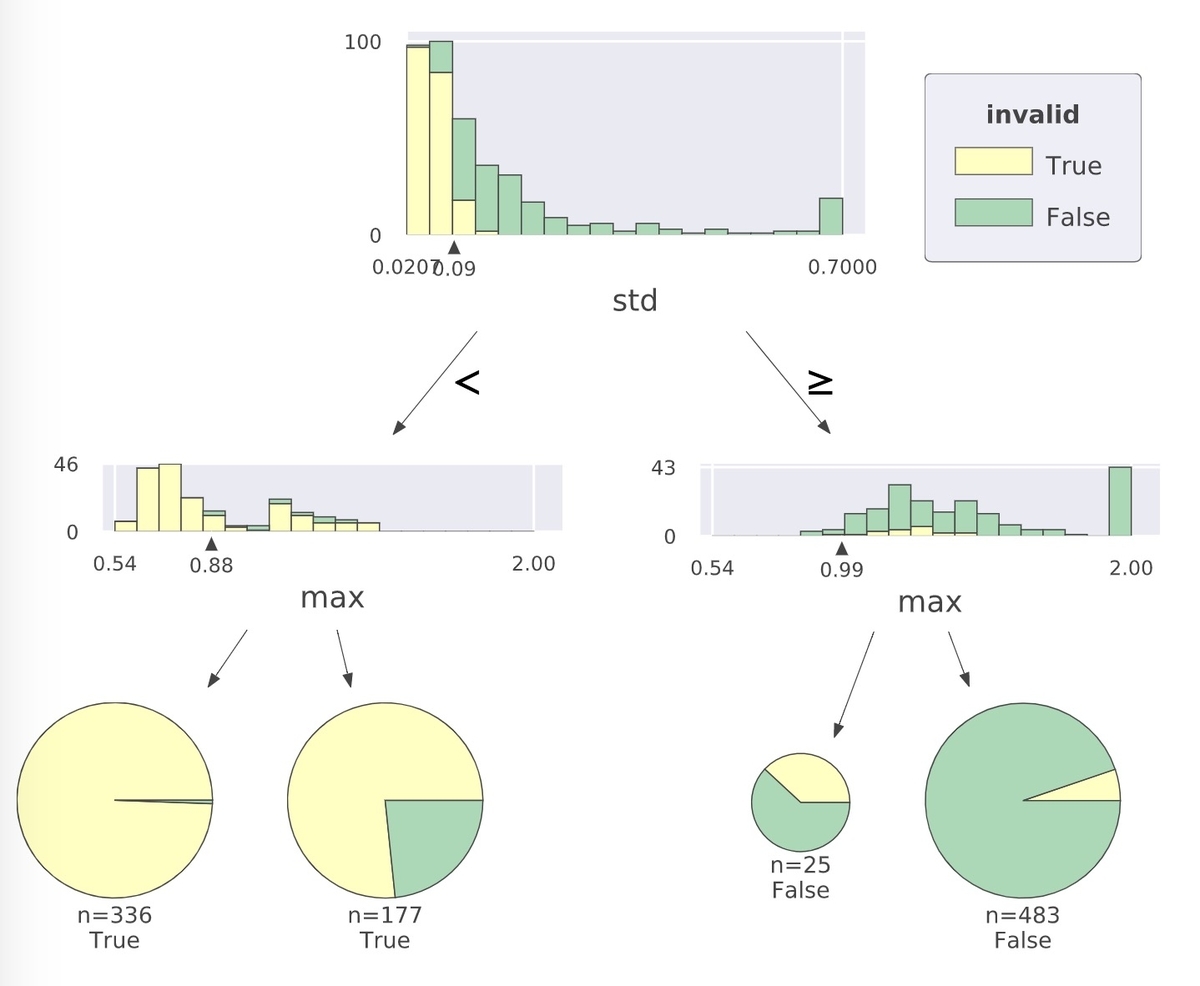
ちなみに、決定木を可視化するためにdtreevizという素晴らしいライブラリがあります。最大値と標準偏差のみで分類を行った際に学習した決定木の一つを可視化した例が下記です。標準偏差が0.09未満かどうかで分類した後に最大値によってさらに分類を行い、それぞれの分岐で正常例や異常例がどんな割合で含まれるかがよく分かります。学習したモデルの妥当性の確認や、推論結果の根拠を説明する際にとても役に立つと思います。
まとめ
ランダムフォレストを用いて時系列データの分類精度を80%から96%まで高めることができました。実はこの後にXGBoostなどのブースティング手法や、深層学習であるLSTMを用いてさらなる精度改善を図る予定でしたが、ブログの執筆期限がすぎているのでランダムフォレストで十分な精度が達成できたのでこれで終わりにします。難しい問題をいかに簡単に解くかが大事。