こんにちは。機械学習やデータ分析に加えて最近インフラ周りにも入門して修行中の浅野です。新しいことにチャレンジするのは楽しいですね。新しいことといえば機械学習の中でも強化学習についてはなかなか手をつけられていなかったので、今回はその強化学習を使って何かを作ってみたいと思います。息子が野球をやっていることもあり、「シチュエーション別の打率データから最強の打順を求める」という課題設定にします。通常は解くべき課題に対して最適な解法を選択していくのが筋ですが、今は「理解を深めるために強化学習をオリジナルの課題に使ってみたい」というのがモチベーションなので、強化学習を使うのが適切か、そもそも解けるのか、といったところはあまり気にせず探索していきたいと思います。
長くなりそうなので次のように2回に分けてまとめていく予定です。
- 前編:打率データの作成とシミュレーション環境の構築 ← いまココ
- 後編:強化学習モデルの学習と評価
強化学習としての大まかな問題設定
強化学習では、ある環境においてエージェントが観測した状態をもとに行動を起こし、それによって得られる報酬の累積値を最大化するような行動指針を学習していきます。今回の課題では、9人の打者のシチュエーション(アウトカウントとランナーの有無)別の打率データがあるとき、ランダムな打順からスタートしてある二人の打順を入れ替えていき、得点力がなるべく大きくなるような打順を求める、という立て付けを考えています。強化学習の枠組みに照らし合わせると、打順が状態に対応し、打順の中で1組を入れ替えることが行動にあたります。報酬については、与えられた打順で各イニングの攻撃をシミュレートし、1試合(9イニング)で得られる総得点をもとに設計していくつもりです。まだこのモデル化が良いのかどうか定かではありませんが、この前編ではそれを検証する上で必要になってくる打率データの生成と得点シミュレーション部分の作成について書いていきます。後編ではそれをもとに実際に行動モデルを強化学習によって求めます。
打率データ
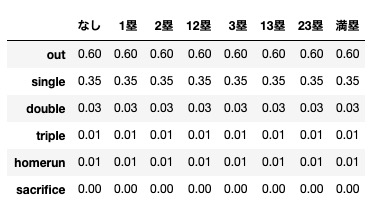
上図はある打者の状況別の打率を定義したものです。ランナーがいるほうが一般に打率が高くなりますが、この打者はランナー状況によってヒット(single), 2塁打(double)、3塁打(triple)、ホームラン(homerun)、犠打(sacrifice)、アウト(out)の割合は変化しない設定です。どんな状況においても35%の確率でシングルヒットを打ち、3%の確率で2塁打、3塁打とホームランは1%ずつです。犠打は行いません。1人の打者に対してこれをアウトカウントごとに定義します。それを9人分作成します。ノーアウトかワンアウトでランナーがいれば高確率で犠打を成功させる川相タイプ、満塁になると異常に打率があがる駒田タイプ、2塁打が多い立浪タイプなど、いろんなバリエーションの選手を用意します(例えが昭和ですね)。一般にツーアウトになると投手が有利なので打率を全般に下げたりするなどの調整も自由ですし、現実のデータを利用することも可能です。今回準備した9人のラインナップは下記のような感じです。
- リードオフマンタイプ:ランナーがいないときの出塁率が高い
- 川相タイプ:犠打の成功率が高い
- 高打率タイプ:どんな状況でも出塁率が高い
- 三冠王タイプ:長打も含めてとにかく打つ
- 駒田タイプ:満塁に強い
- 立浪タイプ:2塁打が多い
- ランスタイプ:打率が極端に低いがホームランだけは多い
- 守備の人: 全体的に打率が低い
- ジョーカータイプ:なぜかツーアウトになると打ちまくる
試合における得点数のシミュレーション
ある打順が与えられたとき、1回の先頭打者から1人ずつ上記で定めた打率データに基づいてアクションを選び、アクションに応じてアウトカウント/ランナー/得点をアップデートし、3アウトになったらイニングを終了させる。それを9イニング繰り返すことで、その打順で1試合でどれだけ得点することができたのか計算することができます。特に実装が難しい部分はありませんが、アクションに応じてランナーを進塁させたり得点を計算したりする部分は下記のようにビット演算にすることで多少すっきりと書けるので一応例を示しておきます。
def update(self, out, runner, action): if action == 'out': # アウト out += 1 elif action == 'sacrifice': # 犠打:ランナーを1つ進塁(左シフト)してアウトカウントを1つ増やす runner = runner << 1 out += 1 elif action == 'single': # ヒット:ランナーを1つあるいは2つ進塁して1塁走者をおく(第0ビットをたてる) if random.random() > 0.5: runner = runner << 1 else: runner = runner << 2 runner = runner | 0b0001 elif action == 'double': # 2塁打: ランナーを2つあるいは3つ進塁して2塁走者をおく if random.random() > 0.5: runner = runner << 2 else: runner = runner << 3 runner = runner | 0b0010 elif action == 'tripple': # 3塁打: ランナーを3つ進塁して3塁走者をおく runner = runner << 3 runner = runner | 0b0100 elif action == 'homerun': # ホームラン: ランナーを4つ進塁し第3ビットをたてる runner = runner << 4 runner = runner | 0b1000 run, runner = self.get_score(runner) # アクションの結果入った得点を計算 return out, runner, run def get_score(self, runner): run = bin(runner & 0b1111000).count('1') # 第3ビット以上で1がたっているビット数が得点 runner = runner & 0b111 # 第0−2ビットに残っているのがランナー return run, runner
得点力が高い打順の例
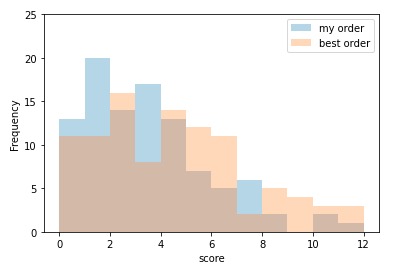
9人で組める打順は9!= 362,880通りです。かなり時間はかかりますが全てのケースで上記の得点シミュレーションを走らせることで、どんな打順が得点力が高いのかを知ることができます。各打順で100試合分のシミュレーションを行い平均得点数を調べてみた結果、私が直感でこんな順番がよいのではないかと思った打順での平均得点は3.05点でした。また、すべての組み合わせの中で最も平均得点が高かった打順では4.03点でした(最低は1.76点)。それぞれの打順を比べてみるとこんな感じです。
| 私の案 (3.05点) | 最高の打順 (4.03点) | |
|---|---|---|
| 1 | リードオフマン | 高打率 |
| 2 | 川相 | 三冠王 |
| 3 | 高打率 | ジョーカー |
| 4 | 三冠王 | 駒田 |
| 5 | 駒田 | 川相 |
| 6 | 立浪 | ランス |
| 7 | ランス | 守備の人 |
| 8 | 守備の人 | 立浪 |
| 9 | ジョーカー | リードオフマン |
平均だけでなく得点の分布も比較してみましょう。水色のヒストグラムが私が考えたオーダーの得点分布で、クリーム色が最高得点の打順の分布です(茶色は両者が重なっている部分)。これを見ると確かに5点以上得点する試合の数がかなり違いますね。
まとめ
打率データをもとにある打順での得点数を算出するシミュレーションが完成しました。対戦相手の能力や相性、ボールカウント、走力、代打、守備力など野球において考慮できていない要素がたくさんありますが、今回は野球の正確なシミュレーション環境を構築するのが目的ではないので気にしないでおきましょう。また、全探索の結果から得点力の高い打順の例を示しましたが、打者の特徴が少しでも変わるたびにこのような計算を行うことは現実的ではないため、後編では強化学習モデルによって得点力のある打順をより効率的に求める手法に挑戦していきます。