決め方の数理 1：検討の数理 - ユニファ開発者ブログ

UniFa プロダクトデベロップメント本部副本部長の西川です、こんにちは。

仕事柄、意思決定に携わることが多いです。
意思決定はその結果がより良い未来につながっていることもあれば、より好ましくない未来につながっていることもあります。
当然、未来に大した影響を与えないような意思決定もあります。

先に意思決定の結果が知れるような魔法の杖でもあればステッキなのですが、残念ながら2021年現在、どのECサイトを覗いてもそんなものは売ってないようです。

では、私たちは何を基準として意思決定を行っていけば良いのでしょうか。
この記事から数回に分けて不定期更新する(心意気の)「決め方の数理」というシリーズは、この問いへの、現時点での私なりの見解をまとめてみようという試みです。
第1回のこの記事、”検討の数理”では、「調査や議論に代表されるような検討には、果たしてどれくらいコストを投じるのが適切なのか」をテーマに語ってみたいと思います。

…と、その前に採用の宣伝をさせてください。 herp.careers プロダクトマネージャ、システムアーキテクト、Rubyエンジニア、Swiftエンジニア、Kotlinエンジニア、Infraエンジニア、QAエンジニア、様々なポジションがあなたをお待ちしております。ぜひぜひ、お気軽なコンタクトをよろしくお願いいたします。

では、始めます。

TL;DR
前提整理：検討によって得るモノ・コト＆費やすモノ・コトの数式化
- 検討で何を得るのか
- 検討は何を費やすのか
  - 検討のコスト
準備処理：検討が価値を生む条件の明確化
- 検討が価値を生む条件の第1表現：当たり前のROI
- 検討が価値を生む条件の第2表現：形式的操作を通じた必要十分条件の抽出
  - (変化後の値 - 変化前の値) ÷ 変化前の値 = 変化率
本題：”検討すること”の価値の見極め
終わりに

TL;DR

検討が価値を生むのは「予測未来価値の期待値変化率 - 今後発生コストの期待値変化率 > 0」な時
上記の「今後発生コストの期待値変化」には検討すること自体でのコスト増も含む

傾向としては、

検討前の予測未来価値期待値が大きいほど、新たに検討する価値は出にくく
検討前の今後発生コスト期待値が大きいほど、追加で検討する価値は出やすい
期待値の変化率なので「確率」に注目するとペイしやすい
検討前の今後発生コストは終盤に近づくほどそもそも小さくなる
なので議論・調査はなるべく序盤寄りが吉(序盤を抜けたら走り抜けるスタイルが吉)と出やすい
なので特に「大きな効果を狙うそれなりの規模の投資についての勝算根拠の確認」はペイしやすい
逆に「やる前から投資規模が小さく押さえられることが分かっている案件」は検討するより走ってしまった方が吉と出やすい

…と私は考えています、ということを、これから長々と書いていきます。

前提整理：検討によって得るモノ・コト＆費やすモノ・コトの数式化

タイトルに「数理」と入れたからには、数学的に考えねばタイトル詐欺です。
私にとって数学とは、

真と仮定することを合意された前提から
形式的な操作・変換を通じて
人類にとっては非自明な情報を
抽出(≠ 創造)する

試みです。

したがって、数理的思考を進めるには、まず前提への合意が必要となります。
また、その前提は直観的に合意できるものでなければなりません。

そのような訳でここから、
「当たり前のことを小難しく表現しただけ」
と感じられるような記述が少しの間、続きます。

ご辛抱してお付き合いいただければ幸いです。

検討で何を得るのか

それでは、まずはここから始めてみましょう。
私たちが検討を行う目的は何でしょうか。

「自己満足だ」という人もいるかもしれません。
が、先も長めなので結論を急ぎます。
ほとんどの場合は、
「より価値ある未来へとたどり着くことが検討の目的だ」
と表現できるのではないでしょうか。
(以下、そんなことはない！という声はなかったものとして話を進めます)

抽象度が高すぎて無意味な記述に見えるかもしれません。
が、そんなことはありません。

未来には価値があること
その価値の増大が検討の目的であること

が分かります。

さて、増大させるためには未来の価値とは何なのか、定義がないと困ります。
それもできれば、ブログのタイトル的に、数理で扱いやすい定義が良いです。

「価値」の定義

価値とは何なのか…という問いは大変面白い哲学的議論です。しかし、ながーくなるので今回は深入りを避けます。
いつかどこかで語るかもしれません。

今回は何らかの方法で価値(Value)を $v$ というように数値化できたとします。

「価値観は人それぞれ、したがって価値の客観的数値化など不可能」
という声も聞こえてきそうです。
私もそう思います。
価値を絶対値として客観的に数量化することなど不可能に思えます。

では、主観的な数量化はどうでしょう？

晩ごはんにハンバーグが出てくる嬉しさが私にとって100カチだとしたら
娘が私のために歌をうたってくれる嬉しさは私にとって53万カチです*1

カチという単位は全くの適当でつけたものです。
しかし、これなら細かく正確には無理でも、ざっくりと数量化することはできそうです。

「こんな主観的な数量化に何の意味があるのか」
という声も聞こえてきそうですが、実は意味があるのです。*2
最後まで読んでいただければ、それに納得していただけると思います(多分)。

「未来の価値」の定義

価値を数量化すれば、期待値の考え方で「未来の価値」も定義できます。

起こりうる未来シナリオが1番目, 2番目, 3番目 ,..., n番目まであったとします。

各シナリオが実現した際に得られる主観的価値を $v_1$ , $v_2$ , $v_3$ ,..., $v_n$
各シナリオが実現する主観的確率を $p_1$ , $p_2$ , $p_3$ ,..., $p_n$ *3

と、それぞれします。
この時、

未来価値の主観的期待値 $F = v_1 \cdot p_1 + v_2 \cdot p_2 + ... + v_{n-1} \cdot p_{n-1} + v_n \cdot p_n = \sum_{i=1}^{n} v_i \cdot p_i$

と表現できます。

$F_x：x$ の場合に今後得られる合計価値の主観的期待値

と表現することにしましょう。

検討の効用

検討が「より価値ある未来へとたどり着くこと」を目的とするものであるならば、その結果は未来に得られる価値の期待値 $F_x$ を変化させるはずです。

検討前時点の予測未来価値の期待値を $F_b$ (before)
検討後時点の予測未来価値の期待値を $F_a$ (after)

と置けば、*4

検討の効用 $\Delta F = F_a - F_b$

と、検討の効用(嬉しさ)を数理的に表現することができます。
$\Delta$ (デルタ)は差分であることを示す記号だと思ってください。

検討は何を費やすのか

「No pain, No delight!」はX JAPAN
「手に入れるために捨てるんだ」はBUMP OF CHICKEN

ですが、とかく何をするにしても(何をしないにしても)、何らかのコストが付きまとうものです。
ここでいうコストは金銭はもちろん、時間、肉体、精神的なコストまで含む、広範な意味での「コスト」だと考えてください。
このコストも、価値と同様に「主観的になら」あらゆるコストが数量化可能です。

ところでですが、時間を巻き戻すことは(少なくとも西暦2021年の人類には)できません。
つまり、支払ったコストは戻ってきません。
過去のコスト、いわゆるサンクコストについてはもう気にしてもしかたがありません。
考える意味があるのは、これから発生するコストについてだけです。

なので、これ以降この記事で登場するコストはすべて「これから発生する未来のコスト」について語っているものと受け止めていただけたらと思います。

検討のコスト

さて、検討が「より価値ある未来へとたどり着くこと」を目的とするものであるならば、その結果は未来に変化を及ぼすはずです。
これから発生するコスト合計の期待値も、未来に変化があれば当然に変化するはずです。

そこで、

検討前段階の自然状態でこれから発生するコスト合計の期待値を $C_b$ (before)
検討後段階での今後発生するコスト合計の期待値を $C_a$ (after)

と置いてみましょう。
ここで $C_a$ には「検討すること自体のコスト」も含まれていることにご注意ください。

すると、すべてを見通す神の視点から見た検討コストは、

検討コスト $\Delta C = C_a - C_b$

と表現できます。

準備処理：検討が価値を生む条件の明確化

ここまでで論旨展開に必要な道具立てが揃いました。
改めて特に重要な点だけ整理しておくと、

検討前時点の予測未来価値の期待値 $F_b$
検討後時点の予測未来価値の期待値 $F_a$
検討の効用 $\Delta F = F_a - F_b$
検討前時点の今後発生するコスト合計の期待値 $C_b$
検討後時点の今後発生するコスト合計の期待値 $C_a$
検討の費用 $\Delta C = C_a - C_b$

です。
ここで $ROI = \frac {真水で得た価値(Return)} {投じたコスト(Investment)}$ という観点から、

検討前時点の主観的予測ROIを $\frac {F_b} {C_b}$
検討後時点の主観的予測ROIを $\frac {F_a} {C_a}$

と表すことができます。

また、考えるのは $C_b, C_a > 0$ および $\frac {F_b} {C_b} \neq 0$ の範囲とします。*5

検討が価値を生む条件の第1表現：当たり前のROI

さて、検討が価値を生むということは、検討した結果としてROIが改善することと同義だと言えます。
したがって、
$\frac {F_a} {C_a} - \frac {F_b} {C_b} = \frac {F_b + \Delta F} {C_b + \Delta C} - \frac {F_b} {C_b} > 0$
が、検討が価値を生む条件であると言えます。

何だか、当たり前のことを数式でかっこつけて表現しただけのように見えますね。
現段階では、そのような感想を抱いて当然だと思います。
こんな風にかっこつけた感じで数式表現して、何か嬉しいことがあるんでしょうか。
実はあるんです。

検討が価値を生む条件の第2表現：形式的操作を通じた必要十分条件の抽出

冒頭で私は数学を、

真と仮定することを合意された前提から
形式的な操作・変換を通じて
人類にとっては非自明な情報を
抽出(≠ 創造)する

試みだと表現しました。

数式に表現することで形式的操作が可能となり、新知見抽出の可能性が高まります。
そういう訳で、先ほど得た第1表現 $\frac {F_b + \Delta F} {C_b + \Delta C} - \frac {F_b} {C_b} > 0$ を形式的に操作していきます。

が、「そこは興味ない」って人も多そうなので、操作過程は折り畳んでおきます。

ここを開いたということは、

計算過程にも興味を持った
結果だけ示されても腑に落ちない*6ので検算したい

といった、奇特な方なのだろうと推察します。

そんなあなたが、もし数学苦手でも、順を追って手を動かせば高確率で最後までたどり着けるように、説明はクドいくらい丁寧にしてみました。
「わっ、数式が多い」
とブラウザ・バックを押すのを、今しばし待っていただけると幸いです。

なお、下記に出てくる⇔は A⇔B で、AとBの真偽関係が必ず一致すること、BがAの必要十分条件であることを示します。

まずは $\frac {F_b + \Delta F} {C_b + \Delta C} - \frac {F_b} {C_b} > 0$ を $\frac {m \cdot \alpha F_b} {m \cdot \beta C_b} - \frac {F_b} {C_b} > 0$ と表現することを考えます。
ここで $m$ は分数の約分を考えた係数であり、 $m \neq 0$ です。
つまり $\frac {F_b + \Delta F} {C_b + \Delta C} = \frac {m \cdot \alpha F_b} {m \cdot \beta C_b}$ という恒等式を考えます。
恒等式の性質から $F_b + \Delta F = m \cdot \alpha F_b$ が言えます。
この式を整理すると $\alpha = \frac {1} {m} \cdot \left ( 1 + \frac {\Delta F} {F_b} \right )$ が得られます。
同様に $C_b + \Delta C = m \cdot \beta C_b$ も言えます。
この式を整理すると $\beta = \frac {1} {m} \cdot \left ( 1 + \frac {\Delta C} {C_b} \right )$ が得られます。
ここで一旦 $\frac {m \cdot \alpha F_b} {m \cdot \beta C_b} - \frac {F_b} {C_b} > 0$ に戻って $\frac {m \cdot \alpha F_b} {m \cdot \beta C_b} - \frac {F_b} {C_b}$ を中心に整理します。
$\frac {m \cdot \alpha F_b} {m \cdot \beta C_b} - \frac {F_b} {C_b} = \frac {m \cdot \alpha F_b} {m \cdot \beta C_b} - \frac {m \cdot \beta F_b} {m \cdot \beta C_b} = \frac {m \cdot (\alpha F_b - \beta F_b)} {m \cdot \beta C_b} = \frac {\alpha - \beta} {\beta} \cdot \frac {F_b} {C_b} > 0$ …式①とできます。
さて $\alpha ' = m \cdot \alpha = 1 + \frac {\Delta F} {F_b}$ 、 $\beta ' = m \cdot \beta = 1 + \frac {\Delta C} {C_b}$ と置いてみます。
すると式①は $\frac {\alpha - \beta} {\beta} \cdot \frac {F_b} {C_b} = \frac {\frac {1} {m} \cdot \alpha ' - \frac {1} {m} \cdot \beta '} {\frac {1} {m} \cdot \beta '} \cdot \frac {F_b} {C_b} = \frac {\alpha ' - \beta '} {\beta '} \cdot \frac {F_b} {C_b} > 0$ と置換できます。
ここで $\beta '$ は $\beta ' = 1 + \frac {\Delta C} {C_b} = 1 + \frac {C_a - C_b} {C_b} = \frac {C_b} {C_b} + \frac {C_a - C_b} {C_b} = \frac {C_a} {C_b}$ です。
$C_b, C_a > 0$ の前提から、 $\beta ' = \frac {C_a} {C_b} > 0$ が今回検討範囲内では保証されます。
$\frac {F_b} {C_b} \neq 0$ かつ $\beta ' > 0$ なので、 $\frac {\alpha ' - \beta ' } {\beta '} \cdot \frac {F_b} {C_b}$ の符号は $\alpha '- \beta '$ の符号に従属します。
つまり $\frac {F_b} {C_b}$ > 0 の時には、 $\frac {F_b + \Delta F} {C_b + \Delta C} - \frac {F_b} {C_b} > 0$ ⇔ $\alpha ' - \beta ' > 0$ です。
逆に $\frac {F_b} {C_b}$ < 0の時には、 $\frac {F_b + \Delta F} {C_b + \Delta C} - \frac {F_b} {C_b} > 0$ ⇔ $\alpha ' - \beta '$ < 0 です。
最後に $\alpha '- \beta ' = 1 + \frac {\Delta F} {F_b} - \left( 1 + \frac {\Delta C} {C_b} \right) = \frac {\Delta F} {F_b} - \frac {\Delta C} {C_b}$ です。

という訳で、

検討前時点の予測ROI = $\frac {F_b} {C_b}$ が正(> 0)なら $\frac {\Delta F} {F_b} - \frac {\Delta C} {C_b}$ > 0であることが
検討前時点の予測ROI = $\frac {F_b} {C_b}$ が負(< 0)なら $\frac {\Delta F} {F_b} - \frac {\Delta C} {C_b}$ < 0であることが

検討が価値を生む必要十分条件であることが分かりました。
だから何だって言うんでしょう？

(変化後の値 - 変化前の値) ÷ 変化前の値 = 変化率

$\Delta F = F_a - F_b$ なのでした。
したがって、

$\frac {\Delta F} {F_b} = \frac {F_a - F_b} {F_b} = \frac {検討の結果として変化した後の予測未来価値 - 検討前時点での予測未来価値} {検討前時点での予測未来価値}$

です。つまり $\frac {\Delta F} {F_b}$ =予測未来価値の期待値変化率です。

同様に $\Delta C = C_a - C_b$ でした。
したがって、

$\frac {\Delta C} {C_b} = \frac {C_a - C_b} {C_b} = \frac {検討の結果として変化した後の合算コスト見込 - 検討前時点での合算コスト見込} {合算コスト見込}$

です。つまり $\frac {\Delta C} {C_b}$ = 今後発生コストの期待値変化率です。

以上から、検討前後を考えた時に、

$\Delta R$ = 予測未来価値の期待値変化率 - 今後発生コストの期待値変化率

が、検討の価値を考えるのに必要十分な要素だと、私は考えています。
だから何だって言うんでしょう？

本題：”検討すること”の価値の見極め

$\Delta R$ = 予測未来価値の期待値変化率 - 今後発生コストの期待値変化率
…が肝だということが分かりました。

ようやく、ここからが本題です。
長くなり過ぎたので、ここからは、

検討前時点での予測ROI $\frac {F_b} {C_b}$ > 0

の場合についてのみ考えることにします。*7
この時、検討することに価値が生まれるのは $\Delta R$ > 0となる場合です。

変化率という数式の特性

$変化率 = \frac {変化後の値 - 変化前の値} {変化前の値}$ という定義から、次の3つの特性を抽出できます。

「変化後の値」と「変化前の値」は同じ単位の量でなければならない
逆に揃っていさえすればどんな単位でも構わない
同じ変化量でも「変化前の値」の絶対値の大きさによって「変化率」の絶対値の大きさも変化する

1.と2.については今回記事の内容の汎用性を支持する特性だと捉えています。
ここで強調すべき特性は3.です。
この特性はどういうことでしょうか。

例えば、検討によって予測未来価値の期待値を1億円大きくできた( $\Delta F =$ 1億円 )とします。
その時、

検討前の予測未来価値の期待値( $F_b$ )が2億円であったら変化率は $\frac {1億円} {2億円}$ = 50% です
検討前の予測未来価値の期待値( $F_b$ )が200億円であったら変化率は $\frac {1億円} {200億円}$ = 0.5% です

というように、同じ量の予測未来価値期待値の変化でも、元々の予測未来価値期待値の大きさによって変化率が異なります。

同様にコストについても見てみましょう。例えば、検討によって今後発生コストの期待値が100時間増えた( $\Delta C =$ 100時間 )とします。その時、

検討前の今後発生コストの期待値( $C_b$ )が200時間であったら変化率は $\frac {100時間} {200時間}$ = 50% です。
検討前の今後発生コストの期待値( $C_b$ )が2,000時間であったら変化率は $\frac {100時間} {2,000時間}$ = 5% です。

というように、同じ量の今後発生コスト期待値の変化でも、元々の今後発生コスト期待値の大きさによって変化率が異なります。
予測未来価値期待値の変化量 $\Delta F$ や今後発生コスト期待値の変化量 $\Delta C$ ではなく、検討前の状態を示す $F_b$ や $C_b$ の影響に着目するというのは、一定の知見ではないかなと自分では思っています。

検討前の状態に基づく傾向整理

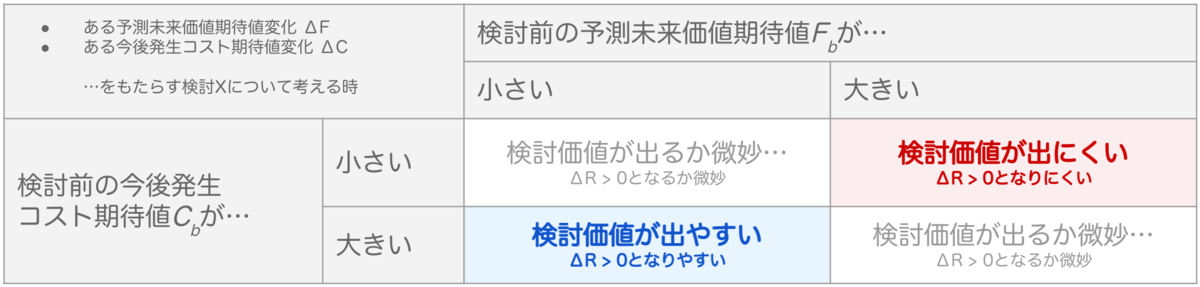
変化率の特性をもとに考えると、次表のように傾向が整理できます。

日本語で表現すると、

検討前の予測未来価値期待値が大きいほど、新たに検討する価値は出にくく
検討前の今後発生コスト期待値が大きいほど、追加で検討する価値は出やすい

という傾向を数式は示唆しているのだと思います。*8

見ているのは「期待値」であるということ

ここで重要になるのが $F_b$ や $C_b$ は期待値であるということです。
期待値は、「場合」ごとの値と、その「場合」の発生確率の、すべての場合についての合計値です。

さて、検討前の予測未来価値期待値が大きいほど、検討価値は出にくいのでした。
では、大きなメリットもありうる話については、検討する価値は出にくく、とっとと行動に移った方が良いのでしょうか？

反語的な問いかけなので答えに予想がついた方も多いかと思いますが、答えは「そう判断するのは早合点」です。
確率を考慮すると、検討前の予測未来価値の期待値 $F_b$ が実は小さかった…というケースは珍しくありません。
人の脳は確率を推し量るのが苦手で、夢を見ている時にはしばしば発生確率レアなベスト・シナリオが約束された未来かのように思えてしまうからです。

大きな予測未来価値期待値を持つトピックは、往々にして求められる投下コストも大きくなりがちです。
そのため、そのようなトピックについて「本当にそううまく行くのか？」と確率を入念に検証するような検討は、価値を持ちやすいと私は考えています。

気にかけるべきコストは「今後発生するコスト」であるということ

また、 $C_b$ も $C_a$ も、どちらも今後発生するコストについて言及したものでした。
そのため、例えばある巨大なプロジェクトについて考えてみると、

開始前時点では $C_b$ がかなり大きくても
終盤近くでは $C_b$ が自然と小さくなっている(残期間が少ないので)

ということが当然のように観察されます。

ここから私は、

真剣に重々しく検討したり方向転換を考えるのならできるだけ序盤がいい
中盤・終盤に差し掛かるほど悩んだり迷ったりにコストを支払うよりは一旦走りきった方がペイしやすい

というようなことを(あくまで傾向としてですが)考えています。

特に検討価値が生まれやすいパタン

まとめると、

大きな効果を狙ったそれなりの規模の投資を伴う案件についての
走り始める前に勝算の根拠を入念に確かめるような検討

…は特に検討価値が高いと私は考えています。

逆に、

やる前から投資規模が小さく押さえられることが分かっている案件
投資規模の大きい案件だが、もう終盤に差し掛かっている案件

については検討価値が出にくいと考えています。

終わりに

今回の検討で用いた $F_x$ や $C_x$ は、あくまで主観的な期待値です。
したがって、今回ご紹介したような指針に則ったとしても、実際にあるトピックについて検討する価値を見出すか否かは、人と状況によって千差万別です。

では今回ご紹介した内容は無意味なのでしょうか？
私はそう思っていません*9。

この指針は、

自分があるトピックについて検討価値を見出した時
自分があるトピックについて追加検討の価値を見出さなかった時

それぞれに置いて、自分が何をどう考えたのか、自分の結論の裏に潜む暗黙的な主張を、自分自身が理解する手助けになってくれると思うからです。
自分が考えていること、しようとしていることが、果たしていったい何を意味するのか。
私としては、それを理解することが質の高い意思決定・学習の第一歩だと考えています。

herp.careers ユニファでは、自分の思考・行動の暗黙的な意味を見つめてやまない開発メンバを大募集中です。プロダクトマネージャ、システムアーキテクト、Rubyエンジニア、Swiftエンジニア、Kotlinエンジニア、Infraエンジニア、QAエンジニア、様々なポジションがあなたをお待ちしております。ぜひぜひ、お気軽なコンタクトをよろしくお願いいたします。

脚注

*1:おそらく他の人にとっては全く違う数値・単位でしょう

*2:似たような考え方にミクロ経済学で云う「効用」などがあります。

*3: $p_1$ + $p_2$ + $p_3$ + ... + $p_n$ = 1 = 100%です。

*4:aとbの割り振りには大分悩んだのですが、アルファベットに準ずるよりも意味想起に期待した方が混乱しにくいかな…と思ってこうしました。

*5:何らかの価値を得る活動にはコストがかかるというう命題が真ならば $C_b = 0$ や $C_a = 0$ は何も価値得る活動をしないことを意味し、考慮外としても問題ないと考えています。また $\frac {F_b} {C_b}$ = 元々のROIが0になるというのは、 $C_b > 0$ から $F_b = 0$ である時ですが、これは $F$ や $v$ の定義を元にして考えると $(G_s - C_s) \cdot p_s + (G_f - C_f) \cdot (100\% - p_s)$ がぴったり0となる場合で、なかなかにレアケースなので言及を諦めても実務上問題がないと考えています。