UniFa プロダクトデベロップメント本部 副本部長の西川です、こんにちは。
最近はなんか妙に暑かったり、かと思えば急に寒くなったりで、大人も子どもも風邪を引きやすいリスキーな季節ですね。 風邪を引きやすい小さなお子さんがいる方々にも安心して働ける環境作りの一環として、弊社では「子どもの看護休暇」という制度を設けています。 1年に10回まで、未就学のお子さんの看病に使うことができるという有給の特別休暇です。
…という採用PRなのですが、弊社では子の有無、婚姻の有無に関わらず多様なバックグラウンドのメンバを絶賛募集中です。 よく聞かれるご質問なのですが、家族の幸せを生み出すあたらしい社会インフラを世界中で創り出そうとしている弊社においても、多くの独身社員が活躍しています。
多様な「家族」のあり方に寄り添い、毎日少しずつ働きやすい環境にしようとがんばっていますので、ちょっとでもユニファでの仕事に興味がある方はぜひぜひお気軽にお声がけください。
さて、本日のタイトルは前回の検討の数理に続く「決め方の数理」第2弾、勝率の数理(AND編)です。
まさか本当に書く日が来るとは。
テーマとしてはざっくり「なぜ戦略はシンプルでなければならないのか?」という問いについて考えてみる形で進めていこうかな、と。
(迷い迷い、手探りで書いてます)
TL;DR
- シンプルに説明できない戦略は、成功確率が数理的に低い。
- 観察・分析が不足している時ほど「シンプルに説明可能な戦略」は描きやすいが、それは弱いシンプルさ。
- 「強いシンプルさ」のためには戦略成功の必要条件をきちんと洗い出し、その厳しさと向き合って、泥臭くシンプルさに「たどり着く」過程が必要。
と、私は思います…的な内容が、以下長々と続きます。
サイコロは何個ある?
サイコロを振って、出た目がすべて2以上だったら勝ち…というゲームについて考えてみます。
サイコロの数が1の時の勝率について考えてみましょう。
6個のケースのうち2か3か4か5か6が出ればいいので… ≒ 83%です。
慣用句に“十中八九”という表現がありますが、サイコロ1つを振った時に2以上が出るのは、十中八九確からしいわけです。
では、サイコロの数が2個、3個、4個…と増えていったときの勝率はどのような感じでしょうか?
それはこんな感じです。
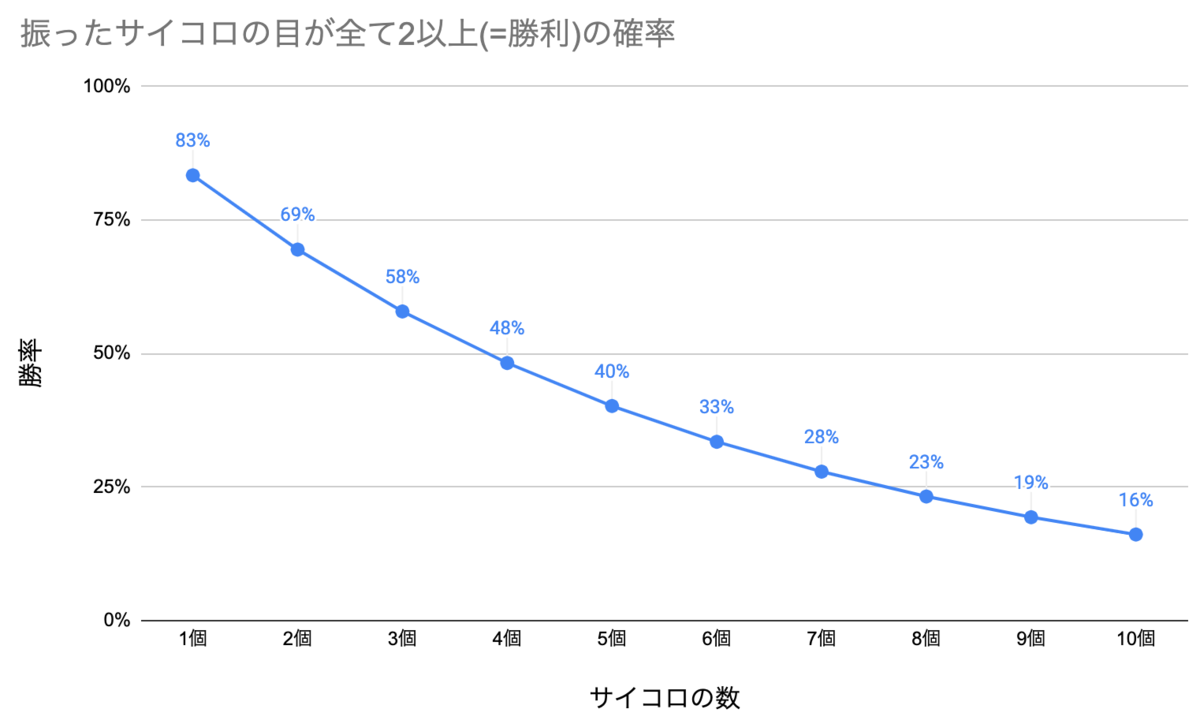
どうしてそう思うかを、次の節から説明していきます。
成功した ⇒ 成功のための必要条件が全て満たされた
「⇒」は“ならば”を意味する論理記号です。
なので、セクションタイトルを日本語にすると「成功したならば、そのための必要条件は全て満たされていなければならない」となります。
これは必要条件の定義から当然というか何というか、必ず正しいと言い切れることです。*1
ここで、成功のための必要条件が全て満たされた ⇒ 成功した…は必ずしも成立するわけでないことに注意してください。
- 成功の必要条件をひとつでも欠いていたら成功しない(対偶)…は絶対に成立しますが
- 成功の必要条件をすべて満たしたら必ず成功する(逆)…と考えるのは数学的に間違っています
図で分かりやすく説明できるので、かんたんに「どうして?」という部分を整理しておきましょう。
A⇒Bということは、ベン図を用いると「Aの枠内に入っているからには絶対Bの枠内に入っている」と捉えられえます。
それを踏まえて、下図を見てください。
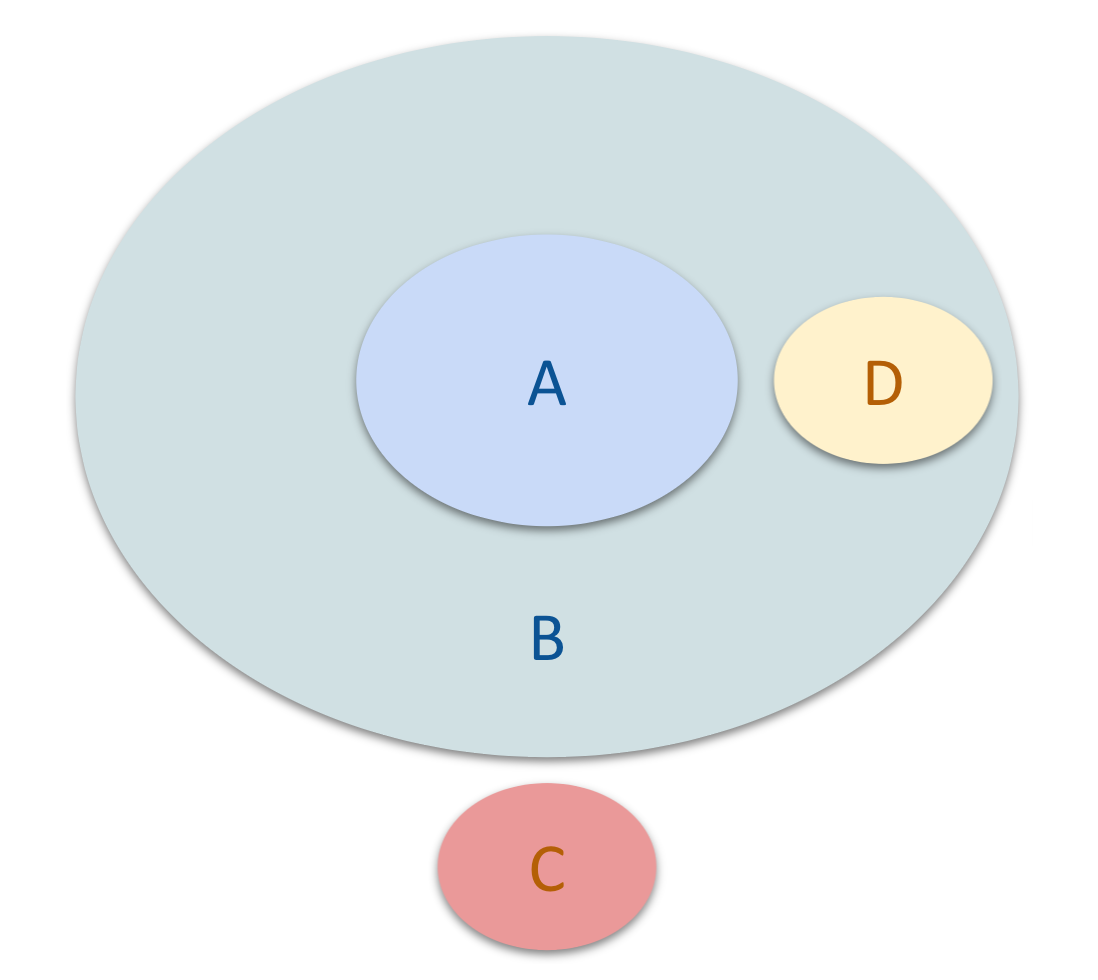
- Cは「Bの外にある」ことを主張しています。この時、絶対にAと重なることはありません。
- Dは「Bの中にある」ことを主張しています。しかし図の通り、Aと重ならずに存在できてしまっています。
- Dは「Aの外にある」ことも主張しています。しかし図の通り、Bの中に存在できてしまっています。
上の図から、A⇒Bが成立する時、対偶(¬B⇒¬A)は絶対にいつでも正しいが、逆(B⇒A)や裏(¬A⇒¬B)は必ずしも正しいとは限らないことが理解できると思います。*2
大事な点を繰り返しておきます。
成功の必要条件をひとつでも欠いていたら成功しない
のです。
サイコロ = 必要条件の数
改めて先ほどのグラフを、見出し通りの視点で見てみましょう。
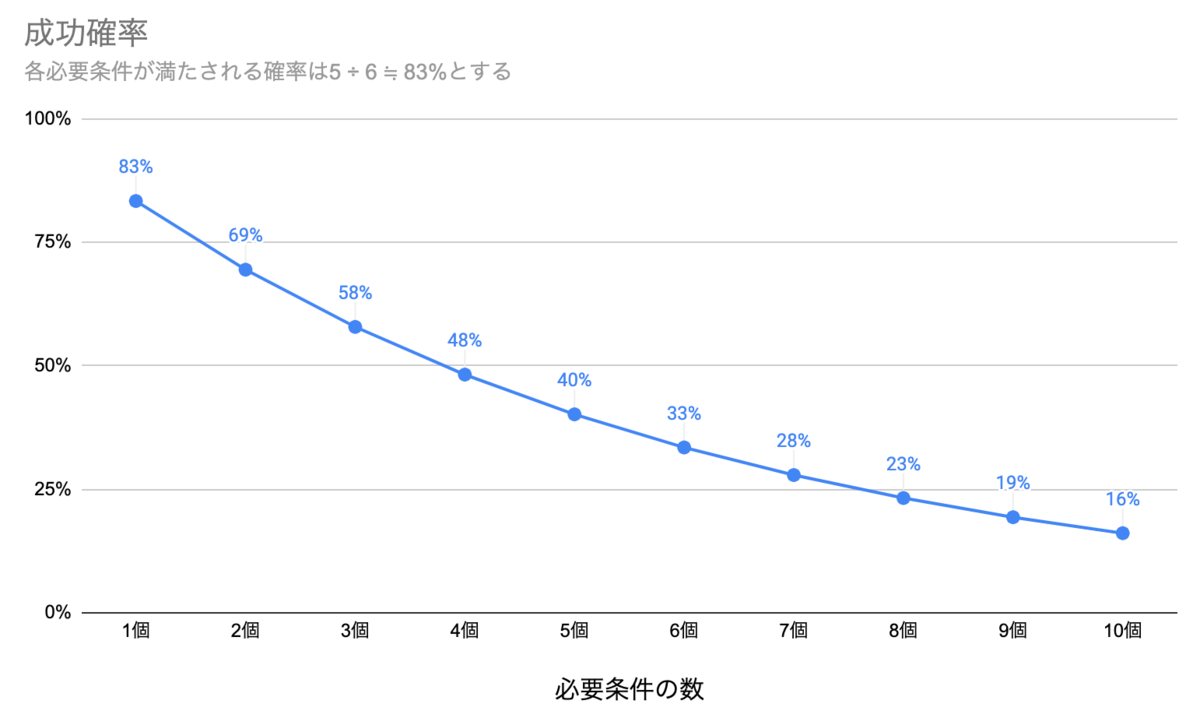
≒ 83% = 十中八九は満たされる条件なのに、それが4つ含まれた時点ですでに勝率は5割を切っています。
さらに9つの条件が含まれると全体の勝率は2割を切り、グラフには描いていませんが条件数13以降は勝率1割未満となります。
それぞれの条件は、たしかに十中八九は満たされる要素なのに…です。
これって、結構衝撃的じゃないでしょうか。*3
戦略がシンプルでなければならないわけ
オッカムの剃刀とマジックナンバ4±1
ここまでで、最初の命題に答える数理的な道具は揃いました。
後は非数理的(科学には関連します)な道具を揃えましょう。
オッカムの剃刀
オッカムの剃刀とは、「ある物事を説明する際に、要素Xがなくても十分にその物事を説明できるのであれば、要素Xを説明に含めるべきではない」的な意味の、説明における指針です。
この記事では考察にあたり、戦略を説明する際にオッカムの剃刀を適用すること…つまり「それがどうであれ勝率に影響のない要素」は説明から省くこと…を前提とします。
マジックナンバ4±1
人が短期記憶に留めておける情報のかたまりは4個±1個程度…という認知心理学的な知見です。
学生時代にはマジックナンバといえば7±2だった気がしますが、より新しい研究では4±1と提唱されていて、現在はそちらが主流の見方のようです。
この記事では、マジックナンバを越える要素数の話について人は「複雑だ = シンプルでない」と捉えると仮定します。
シンプルでない戦略は勝率が低い
戦略の前提
いま、
- 戦略の中には成功の必要条件についての説明が必ず含まれる
- その上で戦略の説明はオッカムの剃刀が適用され、十分かつ必要な最低限度の情報量にまで整理された状態で説明される
ものとします。
「シンプルに語ることができない」戦略は勝率が低い
オッカムの剃刀が適切に用いられた場合、戦略に含まれる内容はすべて成功のための必要条件とみなすことができます*4。
マジックナンバ4±1のセクションでの整理に基づけば、マジックナンバを越えた戦略は、ヒトにとって「シンプルでない」と感じられることになります。
そしてシンプルでない戦略は下に再掲するように、全体の勝率が心許ないものとなってしまいます。
たとえその各要素が十中八九間違いないものであっても、です。

「シンプルに語れれば良い」というわけではない
先ほど見た対偶の考え方を適用すると、ここまで取り扱ってきたのは「良い戦略 ⇒ シンプル」という命題です。
したがって、先ほど見たように
- 対偶: シンプルでないなら良い戦略ではない(¬シンプル⇒¬良い戦略) …は正しい
- 逆 : シンプルなら良い戦略(シンプル⇒良い戦略) …は誤り
です。
サービスやプロダクトづくりでハマりがちな罠
例えば、
- 「左利きの乳幼児*5向けのおしゃれな練習用スプーン」というプロダクトを考えて
- 試作品を作って左利きの乳幼児を育てている世田谷区在住の友人に試しに使ってみてもらったところ
- 「とても良い。左利き用の練習スプーンってなかなかないし、その上かわいい。ちょっと洗いにくいけど、全然気にならないレベル」と好感触の感想をもらった
- そこで量産を考えて色々調べたところ試作品のデザインでは売価2,500円じゃないと粗利が出ない製造原価になることが分かった
- 同時にデザインをシンプルにすれば特徴は失われるものの売価を1,000円程度にまで下げても粗利が出ることも分かった
- そこで試作品を使ってみてもらったところ「多少高くてもこのかわいさがいいんだから、絶対元のままがいい!」と要望を受けた
…というようなケースを考えてみましょう。
この場合「左利きの乳幼児を育てているかわいさ重視の保護者に、かわいい左利き用練習スプーンを提供する」という形で、戦略は非常にシンプルに説明できます。
しかし、この想定顧客である友人には、実は以下のような種々のバックグラウンドがあったとします。

こうして見ると顧客価値が成立するまでに、7〜8個の必要条件が含まれています。
つまり、そのどれもが十中八九間違いないとしても、製品が顧客価値を生み出せるターゲットは2〜3割まで限定されます。
実際には、
- 日本人の左利きの割合は11%ほどと言われていたり
- 子どもがスプーンの練習をする時期は人生の中でごく限られていたり
- 核家族化が進む中で実家が近い世帯の割合はどう高く見積もっても「十中八九間違いない」とは言えなかったり
と、価値が成立するターゲットはすごくニッチに限定されます。
すると何が起こるのかというと、製品をターゲット顧客に認知してもらうまでがめちゃくちゃ大変になります。*6
- 認知されないプロダクトは使ってもらえず
- 使ってもらえないプロダクトは喜んでもらえない
- 使ってもらえないプロダクトは売上もあげてくれない
ので、サービスやプロダクトの作り手としても悲しいし、困った事態になってしまうわけです。
ではどうすれば良いのか?
先ほどのスプーンで例示した戦略は、シンプルではあるけれども、勝ち筋の必要条件をつぶさに洗い出す作業を省いたままシンプルに語られた…という戦略でした。
本当はそうではなく、顧客のペイン・ペイン発生の必要条件・ペイン解消の必要条件をつぶさに洗い出し、その上でシンプルな戦略に落とし込むことが必要なのだと、私は考えています。
具体方法1:「必要条件は何か」をしっかり洗い出す
これはこの後の議論の大前提となりますが、どのように必要条件を洗い出すか…を一般的な形で書くには私の力量が不足しています。
なので、サービス・プロダクトについて考える時に私が使っている自作のフレームワークを紹介します。

感動発生ファネルと名付けたこのフレームワークでは、以下に示す4カテゴリについて十分条件を洗い出し、その充足を勝ち筋の必要条件として読み替えます。
そして各条件が成立する確度・確率を調べ、全体の感動発生確率を調べ、それが思わしくない場合は企画内容を見直したり、泣く泣くお蔵入りさせたりするわけです。
ちなみに上に貼った図は、泣く泣くお蔵入りさせたとある企画案の感動ファネルです。 赤色に着色した条件が、どれだけ頭を捻っても外すこともクリアすることもできませんでした…。
顧客側に設定する条件
- 課題発生条件:顧客においてペインが発生する十分条件
- 一強可能条件:課題発生条件を満たした上で自社商材を1番と評価してくれる顧客であるための十分条件
サービス・プロダクト側に設定する条件
- 価値実現条件:課題発生・一強可能条件を満たして自社商材を購買してくれた顧客に、きちんと約束価値を提供できるための十分条件
- 感動発生条件:価値実現条件が満たされている前提で、顧客が感動してくれそうなシーンを実現するための十分条件
具体方法2:必要条件の確率を「事前に」上げる
各必要条件の充足確率が「十中八九間違いない」 ≒ 83%だとしても、7個連なってしまうと全体勝率は30%にまで下がってしまうことはすでに見た通りです。
ここで、各必要条件が充足される確率を色々変えた時に、必要条件の数に応じた全体勝率がどのように変化するかを見てみましょう。
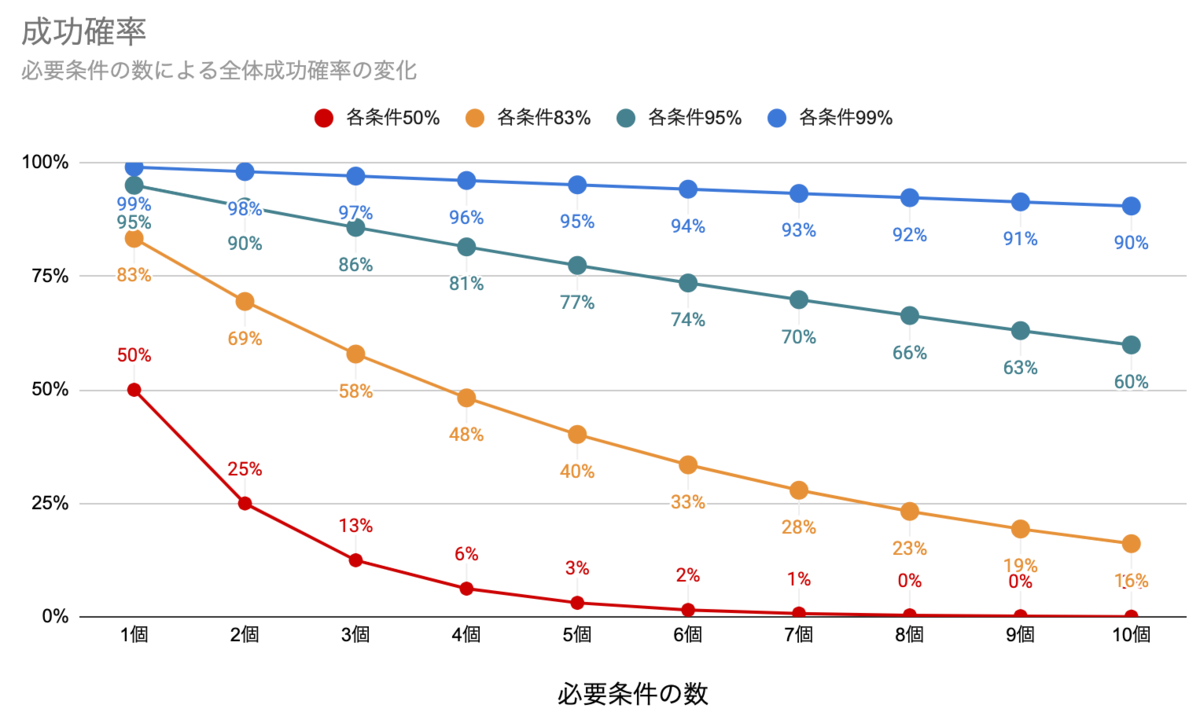
各条件が95%になると、必要条件の追加に対する勝率の変化具合がだいぶ線形に近づきます。
各条件が99%になると、必要条件が10個になっても全体勝率90%を維持できています。
このように、充足確率が95%だったり99%だったりの必要条件は、全体の勝率に対する悪影響が小さくなります。
一方で、各条件が50%の場合、必要条件の数に応じた全体勝率の下がり方は急激で、3つも連なれば勝率は12.5%にまで下がります。
したがって、洗い出された必要条件についてそれが成立する確率を事前に調査しておくことは、たとえそれが十中八九間違いなく成り立つと主観的に思われる場合であっても、非常に意味のある行動*7となります。
合ってるかどうか分からない、チーム内でも議論が分かれる…というような、成否五分五分の項目については、なおさらです。
そして、事前に十分に充足確率が上がった必要条件は、もはや戦略ではなく「充足された事実」として、必要条件から実質的に外してしまうことが可能です*8。
具体方法3:必要条件の数を減らせるように方針転換する
これはセクションタイトルの通りなのですが、1点だけ補足させてください。
戦略や企画の内容を見直さずに、単に必要条件を「なかったことにする」ということではありません。
都合の悪い必要条件に目をつぶって作った戦略のシンプルさは、弱いシンプルさ、手抜きのシンプルさです。
手抜きの代償は後で利子がたっぷりついてから請求が来るものです。
そうではなく、必要条件を外せるように、サンクコストに囚われず、抜本的に戦略や企画を見直す行為を、このセクションでは意図しています。
複雑さを経てたどり着いたシンプルさ = 強いシンプルさ
そろそろ、まとめます。
戦略は、少なくともシンプルに説明しろと言われたら、そうできるものでなければなりません。全体の勝率が低いからです。
しかし本当に良い意味でのシンプルな戦略 = 「強いシンプルさ」を持った戦略は、実は多くの場合、途中で複雑さ(= 情報量の多さ)を経て、その上で最終的にシンプルさにたどり着いているのではないかと、私はそう考えています。
多くの場合に戦略の着想はささいで、単純な出来事です。
その着想を戦略におとす際に、描く戦略がシンプルになるように…という点は多くの人が留意しているポイントでもあると思います。
しかし本当に重要なのは一度シンプルな戦略を描けたその後に、
- 戦略が成功する必要条件を洗い出し
- 各必要条件の充足確度を検証し
- 全体の勝率を計算し
- 必要に応じて戦略の内容を修正し
- その修正によって増えた戦略の複雑度をどうにか減らせないかと苦悩して
どうにかこうにか強いシンプルさにたどり着くという、エレガントさとは程遠い泥臭いプロセスなのだ…と私は考えています。
そしてこのプロセスは、泥臭いだけでなく、上流工程での進捗を遅くする行為*9なので、「大丈夫かな」「進んでいる実感がないな」と不安になりがちなプロセスでもあります。
しかし一方でまた、それに見合う価値があるプロセスでもあると、私としてはそう感じています。
次回予告
次回は、勝率の数理(OR編)ということで「ORはANDより強し」みたいなテーマで語ってみようかな…と考えています。
大胆さと知的泥臭さを併せ持つ仲間を大歓迎!
最後に唐突な採用PRですが、ユニファでは、
- 知的泥臭さを厭(いと)わないどころかむしろ好き
- その上で大胆な発想を行い
- その精度を小さな失敗の積み重ねで磨いていく
ような動きができるメンバを、職種問わず大歓迎しております。
ぜひお気軽にお問い合わせ・お声がけ・ご応募ください!!
*1:前回も書いたように数理的なアプローチでは「当たり前のことを小難しく表現しただけ」という過程を経なければならないことが多々あります。申し訳ありません。
*2:お子さんに「ねぇ、なんで対偶はいつも正しいって言えるの?」と聞かれたら、ドヤ顔で説明してください。
*3:全然衝撃的じゃなかったらどうしよう…
*4:OR条件の場合、A or Bが成立すればOKという条件についても、AとBを包含できる抽象度の表現Cとすれば必要条件と見なせること、十分条件の記述も「十分条件を達成すること」自体が必要条件となること、十分条件でもなくAND条件でもなくOR条件でもなければオッカムの剃刀によって削除済みであることから…です
*5:実は私の1.2歳になる長男がどうやら左利き。
*6:もちろん、ニッチなターゲットに対してがんばってリーチして、それで成立しているサービス・プロダクトも世の中にはたくさんあります。しかしそのようなサービス・プロダクトは、ニッチ顧客にリーチするまでの広宣費・販促費を十分まかなえるくらい高単価な場合が、私の知る限りほとんどだという認識です。
*7:正確には「調査に費やされるコストが、実行後に失敗した時の損失 + リカバリコストを上回らない範囲では」という注釈をつけなければなりませんが、多くの場合において調査コストの方が断然低くなると経験的に感じています。
*8:この議論では、暗黙の前提として、調査・検証結果がこまめに提供され、周囲の事実認識が揃っている状態を想定しています。
*9:開発全体を考えるとむしろ速くする行為と考えてはいますが。