いらっしゃいませ、本日のご注文は豚ロース?鶏ロース?それとも牛ロース?
これがほんとの三択ロース。
…というわけで、ユニファ 西川が開発者ブログ Advent Calendar 2021の24日目をお送りします。
暖まってまいりました。メリークリスマス🎅
さて、本題に入る前に軽くおさらいしておきましょう。
- AND構造だと要素数が増えるにつれ勝率がすごい勢いで低下していく
- OR戦略は勝率を高めるが並行取組数が増えるにつれコスパが悪くなっていく
というようなことを整理しました。
これは言い換えると、
- 集中投資:成功時のコスパは良いが成功確率は低い … AND戦略
- 分散投資:成功確率は高いが成功時のコスパは悪い … OR戦略
と表現できます。この2つで、何とか良いとこどりできないものでしょうか?
…という話を、本日はやっていきます。
TL;DR
- 成功確率があまりに低い時: 何もせずに撤退
- 成功確率が低そうな時: 「見逃しを恐れるより空振りを恐れた」消極的な姿勢の調査による篩(ふるい)戦略
- 成功確率が高そうな時: OR戦略で収益・収支の最大化を狙いに行く
…というアプローチが有利になりやすいと思います。
&
- 「前に進む挑戦をずっと続けながら、同時にずっと臆病者であり続ける勇気」が大事
- だし、そういう仲間を増やしたくほぼ全職種で絶賛採用ブースト中です何卒
もはや古典な篩(ふるい)戦略
えー、ではでは。コスパの話なので、コストについて考えます。
OR戦略のコスパが悪いのは、全て結果の出た未来からの視点で見ると「失敗した」取り組みについても「成功した」取り組みと同等のコストを投じているからです。
ここで、投下コストの総量は時間経過とともに増えていきます*1。
したがって、ある「取り組み完了よりもずっと前のタイミング」で取り組みの成否を見極め、失敗しそうな案へのコスト投下をその時点で打ち切れば、
- OR戦略の勝率の良さと
- AND戦略のコスパの良さの
それぞれを一定程度取り入れた「良いとこ取り」の戦略ができそうです。

篩(ふるい)は振るって残ったものにコスト投下を続けますが、これは逆に篩(ふるい)を通過したもののみにコスト投下を続けます。
しかし細かな違いはさて置き、これを本稿では篩(ふるい)戦略と呼ぶことにします*2。
この篩(ふるい)戦略は決め方の数理1:検討の数理で確認した、
- 議論・調査はなるべく序盤寄りが吉
- 特に「大きな効果を狙うそれなりの規模の投資についての勝算根拠の確認」はペイしやすい
ということにも適合していて、筋が良さげです。めでたしめでたし。
…で終わらせても良いんですが、数理を名乗るにはちょっと数式味が足りませんよね?
「筋は良さげ」だけで納得せず、ちゃんとその真偽や成立条件を解像度高く把握しないと納得できない…ですよね?
分かります分かります、私もそうです。
それでは、そんな皆さんのご要望にお応えすべく、もう少し解像度の高い議論に足を踏み入れて参りましょう。
道具の準備
- 得られる収益期待値を
- 費やすコストを
(
)
で表すと、ある戦略 における差し引き収支期待値は、
と表せます。
この時、
の両方が成立する時、篩(ふるい)戦略はORやANDよりも優れた戦略と評価できます。
ここで、 は収益期待値なので、
- 成功確率を
(
)
- 成功時に得られる収益を
(
)
と表すと、 と表現できます。
また、コストは成功・失敗に関わらず費やされるので確率をかけた期待値ではありませんが、 には必ず*3
となる正の実数
が存在します。
この は換言すると「成功した時には費やしたコストの何倍の収益を得られるのか」という比率です。
後で登場するので頭の片隅に置いておいてください。
OR戦略収支期待値の定式化
個の取り組み(
)を並行して走らせるOR戦略の収支期待値は、
を各取り組みの平均成功確率
を各取り組みが成功した時の平均の収益の大きさ
とした時に、
と表せます。
AND戦略収支期待値の定式化
AND戦略は のOR戦略と同義です。したがって、
と定式化できます。
篩(ふるい)戦略収支期待値の定式化
篩(ふるい)戦略は、調査期間終了時点で、
- 「いける!成功する!!」となった取り組みのみ最後まで実行し
- 「あれれ…成功しないかもかも?」となった取り組みへのコスト投下はその時点で終了する
という戦略です。
そこで、条件付き確率*4を導入し、
- 調査結果が取り組みの成功を示唆する確率を
- 調査結果で成功を示唆された取り組みが完遂後に実際に成功する確率を
と、それぞれ記載することにします。 で、Aが起きた時にBが起きる確率、です。
また、篩(ふるい)戦略ではOR戦略やAND戦略にはない「調査期間」という考え方が存在します。
この調査期間もコストは発生するはずで、この(n個の取り組みについての)調査コストを と表すことにします。
は、調査コストが全体コスト
の何割を占めるかという比率です。
すると篩(ふるい)戦略の収支期待値は、
と記載できます。
ここで、 はベイズの定理により下記のように表現できます。
ベイズの定理に馴染みがない方にはヨビノリたくみ先生の解説動画を見ていただくのがおすすめですが、かんたんな図示説明をしてみます。
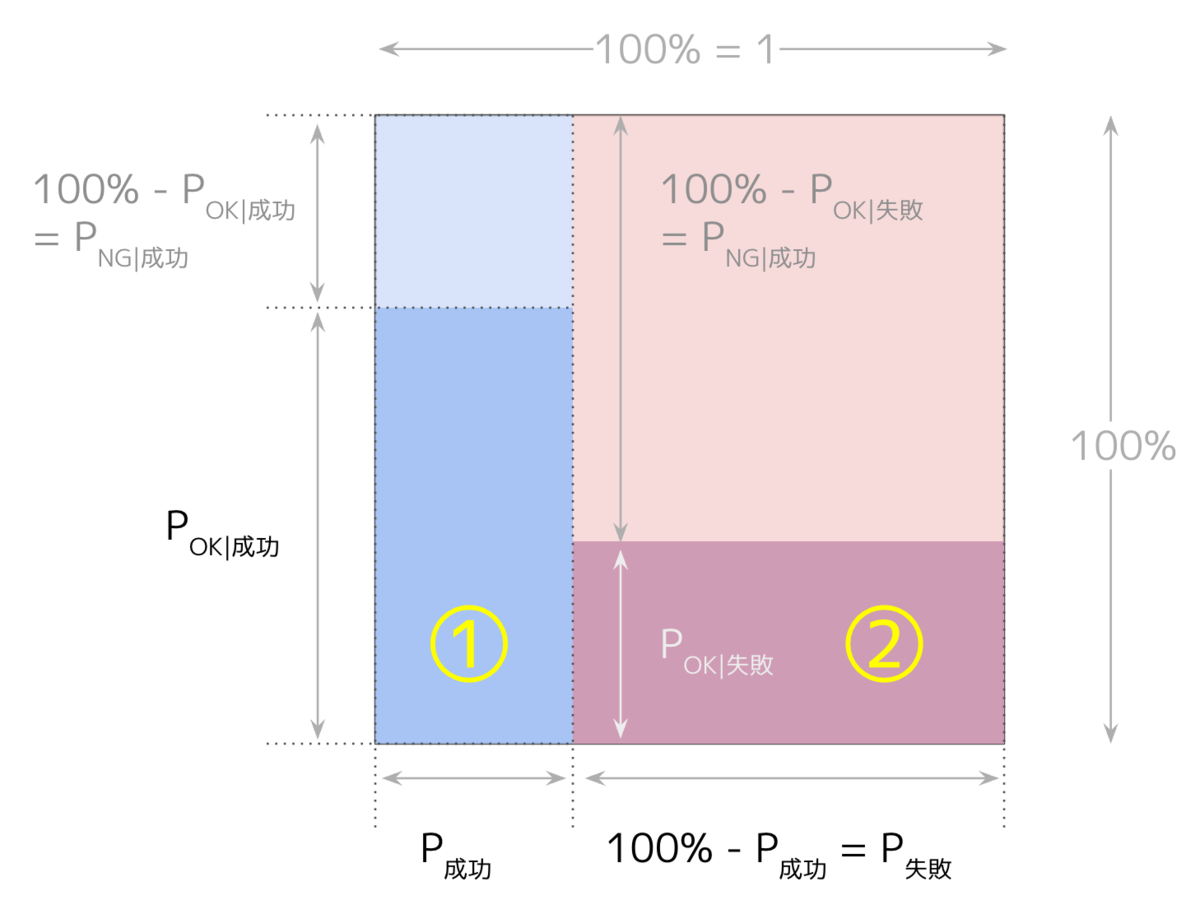
- 調査の結果OKが出るのは上図の①・②です
- ①・②の中で成功するのは①だけです
ゆえに調査の結果OKが出た上で成功する確率は です。ここで、確率を面積と捉えてみましょう*5。すると、①は縦 × 横、すなわち
×
でその面積が求められます。
したがって、調査の結果OKが出た上で成功する確率は、
となります。
これで準備が整いました。
具体例を見てみる
数式いじりの前に、ひとまずこれまでで用意した素朴な状態の式に具体的な値を突っ込んで、結果がどうなるのかを眺めてみましょう。
ヒトによる数式利用が現実世界に意味を持つのは、具体的で実際に即したパラメータが突っ込まれ、その結果がどのような振る舞いになるのかをヒトの脳が言葉やイメージとして捉えられた時だけだと私は考えています。
そのため、数式の解析に先立って数式の出力がどのように振る舞うのかイメージを持つことは、非常に重要だと捉えています。
パラメータの初期値
前回と同様に新規事業について考えてみることにします。
- まず「新規事業の成功」をリクープと位置づけます。
- アビームコンサルティングさんが2018年末に発表した新規事業の実態調査に基づき
と設定します。
から、成功時に得られる収益
が
はないとそもそもリスクに見合った投資になっていないのでキリ良く
(億円) とします。
(億円)が
の中で見合うためには…ということで
(億円) とします。
- OR戦略や篩(ふるい)戦略で並行させるのは
とします。
- 調査コストは全体コストの5%、つまり、
とします。
- 調査は案件が本当に成功する場合は70%の確率でOKを出し(
)、本当は失敗する場合でも30%の確率でOKを出してしまう(
)とします。
- つまり調査の結果OKが出る確率
は
です。
こんな感じのパラメータを初期設定として、適宜「このパラメータを動かした場合はこうです」という形でグラフを示していきたいと思います。
勝率を動かしてみる
他のパラメータは初期値のまま固定して、 の値を推移させてみた時の
と
の動きを見てみましょう。
なので、グラフの見方としては、
- 線が0より上にある ⇒ 篩(ふるい)戦略が対戦相手よりも性能が良い
- 線が0より下にある ⇒ 対戦相手の方が篩(ふるい)戦略よりも性能が良い
です。
さてさて。
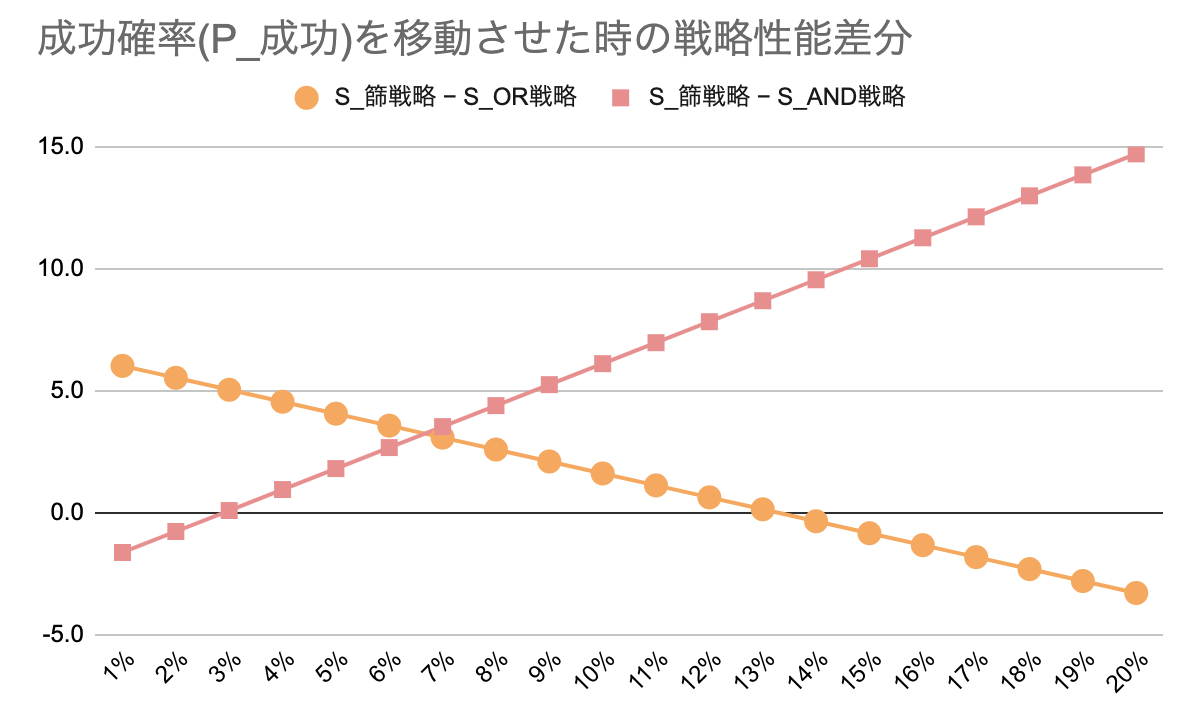
このグラフはこのグラフで中々に味わい深く、例えば、
- 勝率が低い時は余計なことをせずに1点集中の方が(どうせ失敗確率が高い分)傷は浅く済むので得
- 勝率が高そうなフィールドほど複数取り組みを並行させた方が(それらがそれぞれ報われる確率が高いので)お得
ということが示唆されます。
全集中のANDの呼吸よりも、取り組みを並行させるOR戦略の方が効率的という傾向を抽出できます。しかしながら、ヒトは結構この逆をやりがちではないでしょうか? 勝率が低そうな時ほど保険を張りたがるものだし、勝率が高そうな予感を抱いている時には満足して一点突破を選びがちではないでしょうか? そんな気がしますが、どうなんでしょうか? 気のせいかもしれません。 それから、 その他のパラメータが初期値に沿う場合には、おおよそ 他のパラメータは初期値のまま固定して、 その他のパラメータが初期値に沿う場合には、 それぞれ最適な戦略となってきています。 総コスト1億円に対して7%の確率で30億円返ってくる…そんなゲームの場合は、よほど高精度かつ安価な調査がない限りは、篩(ふるい)戦略よりもOR戦略の方が良さそうです。 他のパラメータは初期値のまま固定して、 その他のパラメータが初期値に沿う場合には、調査コストが実行コスト全体の35%を越えるようだと、篩(ふるい)戦略に要する調査コスト & 玉を絞ることによる収益減が圧縮されるコストを上回るので、それは慎重になりすぎですね…ということになります。 さてさて、ここまで具体例を見てイメージを膨らませてきました。 ではでは、数式をいじって要素間の構造的関係性を明らかにしていきましょう。 と言っても、今日のブログでちょっとややこしいかもしれないところはベイズの定理だけで、そこはもう通過済みなので、後はサクサク式変形していくだけです。 ここまで整理した上で、 ⇒ という式を得ておきます。 を得ます。 だから何だって言うんでしょう? まず、式②は篩(ふるい)戦略がOR戦略より高パフォーマンスであるための条件の1つを示しています。 さて、右辺は分数です。したがって、 ことになります。 ということが分かります。
したがって、式②からは下記のような教訓が得られると考えています。 いくのですが、その前に、 を得ます。 だから何だって言うんでしょう? 式②と同様、式③も篩(ふるい)戦略がOR戦略より高パフォーマンスであるための条件の1つを示しています。 さて、その右辺ですが、次のように前半・後半に色分けしてみます。 すると、調査コストの実行コストに対する比率の上限は、青字部分から赤字部分を差し引いた残りであることが分かります。 という感じです。 青字で書いた前半部については、 なので という構造が見てとれます。 赤字で書いた後半部についても、 なので、こちらも正であることが担保されます。 という構造が見てとれます。 また、 出やすいことが分かります。 これらの事柄を整理すると式③からは、篩(ふるい)戦略を採用すると決定した後の調査の仕方について、下記のような教訓を抽出できます。 今日の話を整理すると、 が有利になりやすい…ということになります。ここで、注意が2点あります。 1つは、これらはあくまで数式上の構造であって、現実世界で何が最適な戦略かは、現実世界で取り組む領域・事柄の具体的なパラメータによって変わるということです*8。 もう1つは、ビジネスで「何か新しいことをやろう」という取り組みの成功確率はたいてい低い*9ということです。 最後に、同じように考え、そのプロセスを楽しいと思えて、その上で篩(ふるい)を抜けた案については万難を排して成功まで完遂するような方がUnifaに興味を持っていただけたなら、正直とっても嬉しいです。ということで、採用宣伝です。 QAマネージャ、Appエンジニアをはじめ、デジタルマーケターや営業企画などのBiz職種も含め、ほぼほぼ全方面で採用踏込中です。 ではでは皆さん、よいお年を。明日はCTOの赤沼です。 *1:収益 - 費用で示されるような差引コストの話をしているわけではないことに注意してください。 *2:古典的な篩(ふるい)戦略という駄洒落の語感を大事にしたいからです *3:正確には *4:条件付き確率についてはこちらのページなどが分かりやすいと思います。 *5:確率は面積です。 *6:つまり成功確率が高いと確信できない *7: *8:では、こうして数式をいじくることに意味がないかというと、もちろんあると思っています。が、それを語るとまた長くなってしまうので、以前に書いたこちらの「終わりに」をご参照ください。 *9:アビームコンサルティングさんが2018年末に発表した新規事業の実態調査で、リクープまで行く確率が7%くらい実際に
を念頭に
を整理すると…
…
なので
という式を得られ、
の範囲で篩(ふるい)戦略が(このOR、AND、篩の3つの中では)最適戦略となることがグラフから見てとれます。
成功時のリターン倍率を動かしてみる
= リクープに成功したら
の何倍の
が返ってくるのかという倍率の平均値…を推移させてみた時の
と
は下図の通りです。
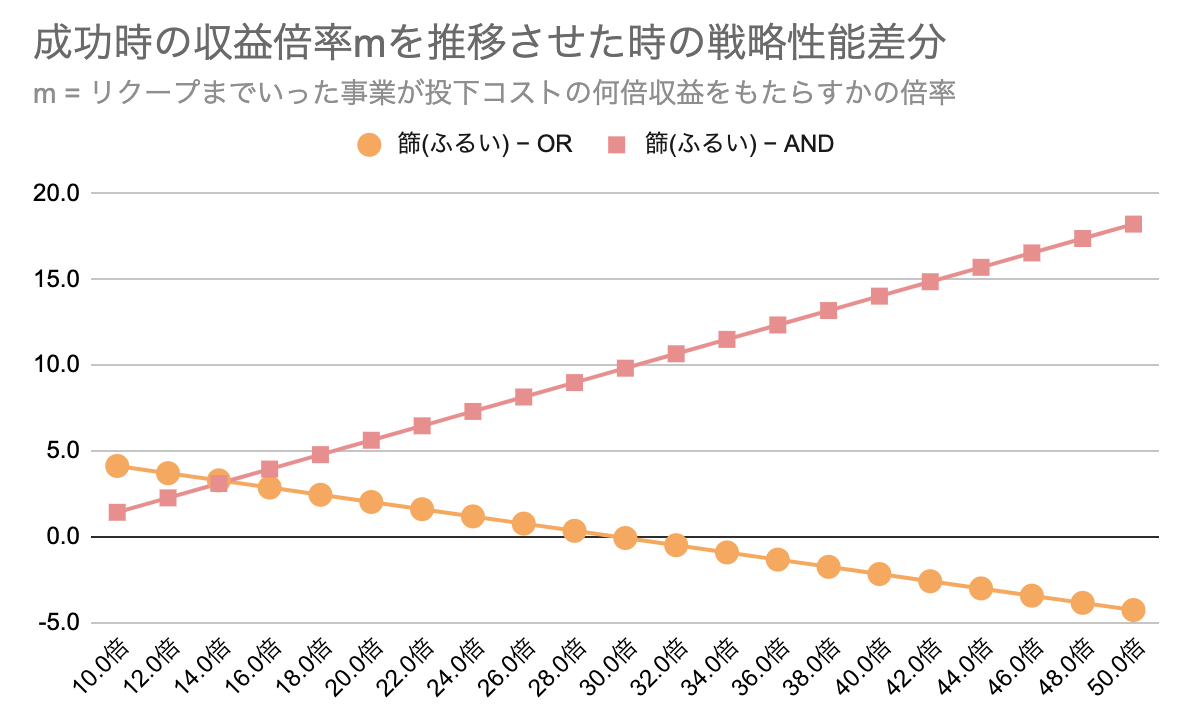
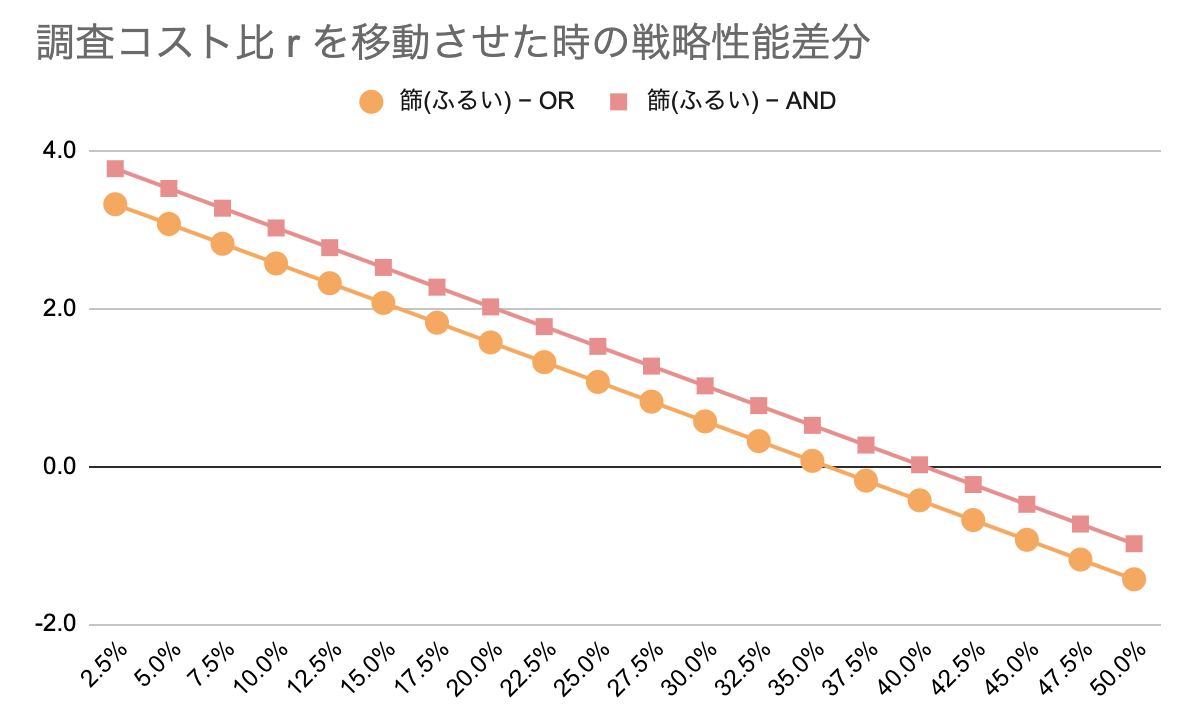
調査コストの大きさを動かしてみる
= 調査コストを
に比べてどれくらいかけるのかという比率…を推移させてみた時の
と
は下図の通りです。
関係の構造を紐解く
まずは
を念頭に
をある程度まで整理して…
だったことを思い出して上式に代入すると、
…式①
篩(ふるい)戦略が有効となる「リターンの大きさ」についての条件
式①を
について整理して…
…式②
それは式②の左辺である取り組みによるリターンの倍率が、右辺の求めるところより小さいことです。
に対し篩(ふるい)戦略の有効性が失われやすい
に対し篩(ふるい)戦略の有効性が保たれやすい
そうした中で であったことを思い出しながら式を見ると…
があきらかに高い話にはそもそも篩(ふるい)戦略は有効性を持ちづらい
= 空振り確率をいかに抑えるかが篩(ふるい)戦略を適用できるmに対して支配的な影響を与える
篩(ふるい)戦略で許容される調査コストの大きさ
式①を
について整理して…
を式①に代入します。
…式③
それは、調査コストの実行コストに対する比である が右辺の求めるところより小さくなければならないという条件です。
つまり、
で、正であることが担保されます。
青字部分については、
が大きくなると青字部分は小さくなる
が大きくなると青字部分は大きくなる
かつ
なので
赤字部分については、
が大きくなれば赤字部分は大きくなる*7
が大きくなれば赤字部分は小さくなる
と
の関係に着目すると、
が大きい = 成功確率の高い領域 …ほど
の増大による
上限の押し上げ効果が大きく
が小さい = 成功確率の低い領域 …ほど
の増大による
上限の押し下げ効果が大きく
)領域では「空振りを恐れるよりも成功機会の見逃しを恐れた」調査にコストを使うのが吉
)領域では「見逃しを恐れるより空振りを恐れた」調査にコストを使うのが吉
まとめ
前に進み続けながらずっと臆病者であり続ける勇気
その中で、でも「挑戦なくして成長なし」という真理から、我々は挑戦を続けなくてはならないわけです。
これは一種の認知不協和で、これを解消するためにヒトの脳は「でも自分たちの挑戦はうまく行く」と信じ込もうとします。
挑戦をしようとする者は成功予測を肯定する声を歓迎し、自身もまた「積極的な挑戦」を推奨する声を発信します。
そのような声の中で慎重な姿勢を崩さないことは、大変な勇気がいることです。
しかし私自身としては、それはそうする価値があることだと考えています。
何卒お気軽にカジュアル面談のお声がけくださいませませ。と
の単位が同一(円、価値の大きさ etc.)かつ実数で表現可能であればという補足が付きます。
の増大に対して
の分で差が広がる感じです。