はじめに
こんにちわ、研究開発部の島田です。
先日、2019年度 人工知能学会全国大会が行われ、なんと弊社はプラチナスポンサーとして協賛し、ブースも出展させていただきました。当日は研究開発部のメンバーが総出で対応を行ったのですが、その際に色々な方から応援メッセージをいただけたので大変嬉しかったです。
学会の参加報告については、Podcastでも公開されていますのでご興味ある方はぜひこちらもどうぞ。
さて、会社としての学会参加の目的はいくつかあるわけですが、その中の一つとして”採用”があります。ですので、ブース対応するユニファ社員の関心事の一つとして、この人は「採用に興味があるのか、無いのか」になります。
採用に興味がある人であれば、出来るだけ短時間でかつ詳細に採用情報について知りたいはずです。そういう人に対しては的確な採用情報をなるべく早く与えてあげるべきですよね。
一方で、採用に興味が無い人に対して、採用情報ばかり提供してもお互いにとって良い時間の使い方にはならないはずです。
採用経験豊富な方であれば、目の前の人がどちらのタイプかをすぐに見極めるられるのでしょう。しかし、私みたいな初心者には無理です。。。それならエンジニアらしく、この直感的な判断を数値化してみよう!と思い立ちました。
ということで、前置きが長くなりましたが今回の記事は、学会のブースに来た人が採用に興味があるか否かを数値化してみたいと思います。
※ただし、本記事で計算に使う各パラメータは全て架空のパラメータとします。
ベイズ推定
さて、目的の数値化のために、今回はベイズ推定を使いたいと思います。
ベイズ推定は、一般的には下記のように説明されます。
ベイズ確率の考え方に基づき、観測事象(観測された事実)から、推定したい事柄(それの起因である原因事象)を、確率的な意味で推論することを指す。
出典:Wikipedia
小難しく聞こえますが要するに、観測されたある事実を使って推定したい事柄を確率的に求める手法のことです。 ベイズ統計学という分野は昔からありましたが、最近また注目を浴びてきました。
例えば、MicrosoftやGoogleなどでもベイズ統計の技術を活かしていることで知られています。
ベイズ統計の特徴(強み)は以下があげられます。
事前知識を取り入れることで、少ないデータでもある程度の精度で推測可能。
入力情報によって瞬時にそして自動的に推測を更新する
逐次合理性が成り立つ
ベイズ推定の流れ
はじめに今回のベイズ推定の処理の流れについて見ていきます。
大まかにはこういう流れで進めていきます。
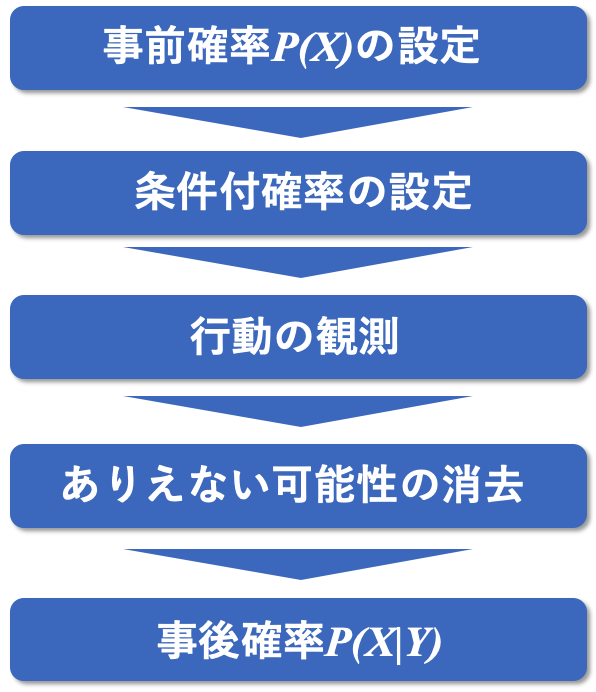
事前確率の設定
今回推定したいのは、ブースに来た人が採用に「興味ある」か「興味ない」かということです。そのために、推定の最初にすべきことはこの二つのタイプに対して、その割合を割り振ることです。この割合は経験に基づく設定の仕方と、そうでない割り当て方がありますが、ここでは、経験から数値が分かっているものとします。
例えば、経験的にブースを見に来た人の中で採用に「興味ある()」割合が10%(0.1)で、「興味ない(
)」割合が90%(0.9)だったとします。そうすると、事前確率は以下のように表せます。
条件付き確率の設定
次に、採用に興味あるかないかの二つのタイプに属する人の中で、それぞれどのくらいの割合でブースにいた弊社社員に「声をかけた」かを設定します。この条件付き確率では何らかの経験による裏付けや実験的な結果(数値)が必須です。ここでは、この結果(確率)も分かっているものとします。
例えば、「採用に興味がある人」は以下のような条件付き確率を設定します。
「採用に興味がある かつ 声をかける(
)」割合が80%(0.8)
「採用に興味がある かつ 声をかけない(
)」割合が20%(0.2)
一方、「採用に興味がない人」は以下のように設定します。
「採用に興味がない かつ 声をかける(
)」割合が40%(0.4)
「採用に興味がない かつ 声をかけない(
)」割合が60%(0.6)
行動の観測、ありえない可能性の消去
前項までの設定をし、実際に学会のブース対応したと仮定します。そしてありがたいことに、ある一人の方に声をかけられたとします。
これは一人の行動を実際に観測したことになり、「声かけしない」という可能性が消えて、確率が変化しました。
つまり、この実際の観測により、世界は以下の二つに限定されました。
「採用に興味ある&声かける」P(A and 声かけ)
「採用に興味ない&声かける」P(B and 声かけ)
それぞれの確率を計算します。
事後確率を求める
では、いよいよ本題である「声かけをしてきた人で採用に興味がある確率」を求めます。
前項にて、観測された事実からありえない可能性を消去し世界が変化したことで、確率の和が1にならなくなりました。
そこで、それぞれの確率の組を正規化(足して1になるようにする処理のこと)を行い、事後確率を求めます。
この結果から、声をかけていただいた人が「採用に興味がある」確率は、約18%であると推定できました。
更に一つ大事なこととして、事前確率の設定の段階で「採用に興味がある人」と仮定したのは、10%でした。 ですが、「声をかける」という実際の事象を観測した後には、その人が採用に興味がある確率は、0.1から0.18と2倍弱にまで値が更新されました(これをベイズ更新と言います)。
このようにデータが与えられる度に値が更新されていくのもベイズ推定の一つの特徴でもあります。
おわりに
ベイズ推定を簡単に応用したケースを紹介してみましたが、いかがでしたでしょうか。
ベイズ推定は実際のビジネスシーンにおいてもかなり幅広く応用できる手法ですので、今後も色々と試してみたいと思います。
また、冒頭でもお伝えした通り、今回のブース出展では大変多くの方に応援のメッセージを頂きました!皆さんの期待を裏切らないためにも日々精進していきたいと思います。